校正の不確かさの算出方法と校正項目による違いについて
EMC試験サイトの管理・運営上、試験システムの不確かさを求めておくことが重要です。
そのためには使用計測器を校正した時の不確かさが必要となります。
当社のキャリブレーションラボラトリーは、高周波測定器の校正におけるISO/IEC 170251)認定を取得しています。また、当社が発行する校正証明書にはISO/IEC 17025規格で要求される「校正の不確かさ」を記載しています。この「校正の不確かさ」について、その「算出方法」および「校正項目による不確かさの違い」について、解説いたします。
1) 国際標準化機構(ISO)によって策定された、試験所および校正機関が特定の試験または校正を実施する能力に関する一般要求事項を規定した国際標準規格。
不確かさの算出
校正の不確かさを求めるためには、まず統計的手法(タイプA)とその他の手法(タイプB)で不確かさを算出します。そしてその合成値を全体的な不確かさとします。
タイプAでは、以下の手順で測定したデータから統計処理を行い、測定値のばらつきを算出します(図1)。
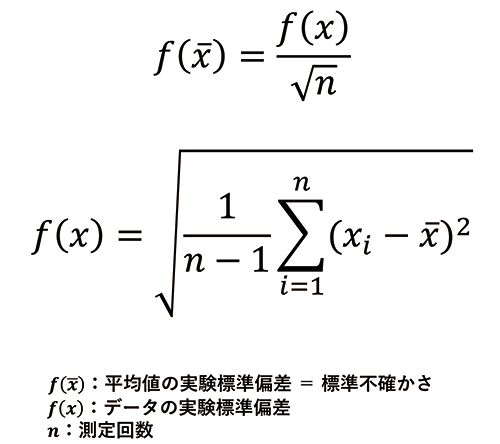
図1:校正の不確かさを求める統計的手法(タイプA)
- 繰り返しデータを測定
- 測定値・平均値・データ数から標準偏差を算出
- 標準偏差・データ数から標準不確かさを算出
タイプBでは、測定で使用している標準器の不確かさ、標準器間のミスマッチといったことが要因で起こる不確かさを算出します。そしてタイプAの不確かさと合成した結果が、最終的な不確かさとなります。
当社では、表1のような「バジェット」と呼ばれる一覧表を使って不確かさを算出し、校正証明書に記載しています。
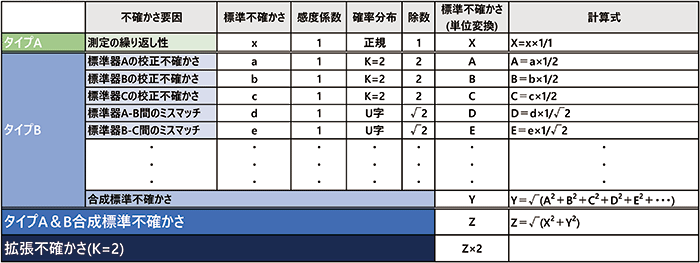
表1:不確かさを算出するための「バジェット」
ここで求めている不確かさは「拡張不確かさ」であり、校正で得られた不確かさにさらに幅を持たせてより信頼性を高めた値です。VIM(国際計量基本用語集)2)で、拡張不確かさは「合成測定標準不確かさと1より大きい定数との積」と定義されています。この定数が包含係数Kであり、K=2は、計算で得られた不確かさを2 倍することを意味し、それにより測定値の約95%が不確かさの範囲内に含まれることになります。なお、包含係数K=1の場合は、決定された信頼の水準が約68%、K=3の場合は約99%となります。校正の不確かさの場合は、一般的にK=2が適用されます。
2) 計量用語の総合的・普遍的な定義としてISOから発行されている。
校正項目による不確かさの違い
校正項目によって、バジェット中の不確かさの要因や標準不確かさが異なるため、校正の不確かさの値も異なります。例えば、アッテネータの校正項目「インサーションロス」は、繰り返し測定のばらつきがほとんどなく、不確かさの要因も少ないため、校正の不確かさも0.1~0.2dBと小さい値になります。一方、電界プローブの校正項目「周波数応答」は繰り返し測定のばらつきがあり、不確かさの要因も多いため、校正の不確かさも1.0~1.5dBと大きい値になります。これは、アッテネータを使用する測定よりも、電界プローブを使用する測定の方が、測定結果のばらつきの可能性が大きくなることを意味しています。つまり、「測定の不確かさが大きい」と言えます。