緩和時間分布解析法の基本原理

モバイルデバイスやエコカーの発展に伴い、電池の重要性はますます増しており、世界中で研究開発が盛んに行われています。電池の電極界面反応を評価する手法の一つとして電気化学インピーダンス測定法（EIS法）があります。以下に紹介する緩和時間分布解析法（DRT解析法）は、EISで得られたデータを解析する「等価回路フィッティング」を数値計算の観点から支援する新たな手法として期待されています。

電気化学系のインピーダンス

EIS法は、微弱な交流信号を入力した際の応答信号から離散フーリエ変換によって電気化学系の複素インピーダンス（実部：Zʼ、虚部：Zʼʼ）を得る測定手法です。

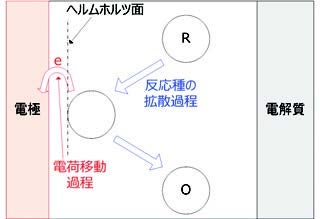
電極界面における反応イメージ

電気化学系の反応では、その素過程毎に応答周波数が異なるインピーダンスとして現れます。この応答周波数の時間場における表現が時定数（緩和時間：t = 1/ω_max = R_ctC_dl）であり、様々な周波数でインピーダンスを測定することにより、電極の反応素過程の詳細を調べることができます。

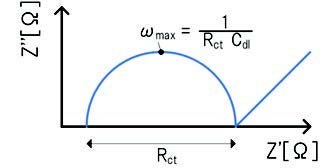
EISデータのナイキストプロットイメージ

複素非線形最小二乗法（CNLS）とその課題

EISデータの解析では、抵抗やコンダクタンスなどから成る等価回路を仮定し、複素非線形最小二乗法（CNLS）によるフィッティングを行うことでそれぞれの分極抵抗成分を分離し定量評価することが一般的に行われています。しかしながら、実際の電池では参照電極を設けることができないケースが多く、複数の分極抵抗成分が入り混じった状態となりCNLS法による成分分離が難しい場合があります。

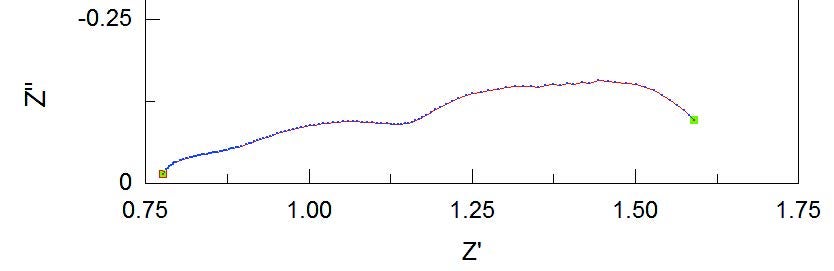
SOFCのEISデータ例

緩和時間分布解析法

緩和時間分布（Distribution of Relaxation Times: DRT）解析法は、周波数場のEISスペクトルを逆フーリエ変換することにより求められる緩和時間分布関数（DRTスペクトル）を用いて、分極抵抗成分を分離する手法です。
DRT解析法では、N個のRC並列回路が直列接続されている等価回路を仮定します。

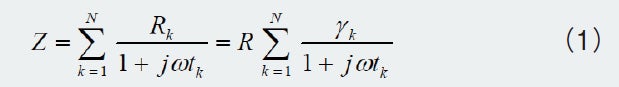
ここでγ_k は緩和時間分布関数を示します。
（1）式を実部と虚部に分離し、さらに式変換を繰り返すと以下が導出されます。

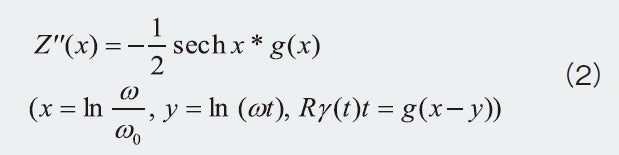
畳み込みの定理および逆フーリエ変換式から緩和時間分布関数g（x）を求めることができます。R-CPE要素の緩和時間分布関数は以下の式で表されます。

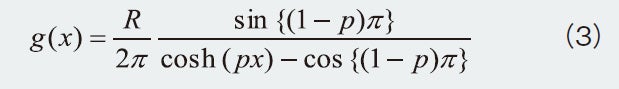
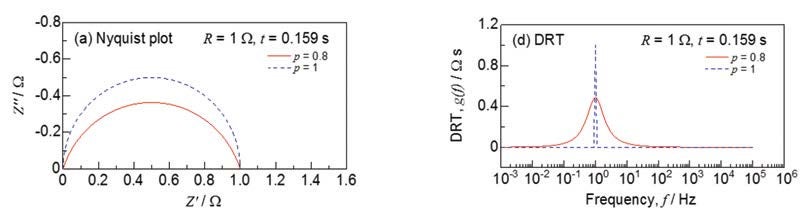
ナイキストプロットとDRTスペクトル

＜実データ解析例＞
冒頭に示した“SOFCのEISデータ”に対して緩和時間分布解析を行い、各分極抵抗成分を求めた結果が下図です。4つの成分（赤・青・緑・黄）に分離できています。

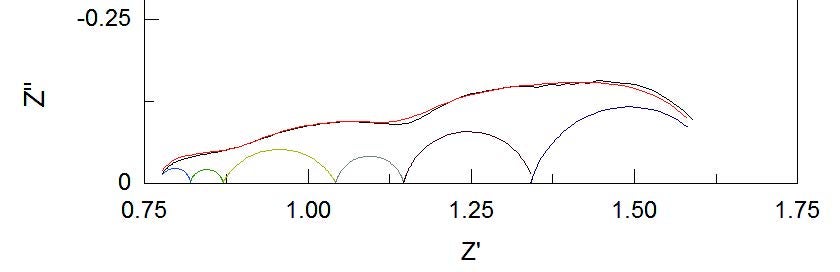
SOFC EISデータのDRT解析結果例

まとめ

DRT解析法を用いることにより、等価回路フィッティングにおける分極抵抗成分の分離をより良く実施できる（可能性がある）ことを示しました。しかしながら、この解析法には適用制限が存在し、以下の点などに注意する必要があります。

① R-CPE並列回路の直列接続のみでは表現しにくい領域（イオン拡散過程など）への適用
② 正則化パラメータλによる影響

※この度、我々は産業技術総合研究所の技術支援を頂き、DRT解析法を適用したソフトウェアを新たに開発しました。

参考文献
・H. Sumi et al., Solid State Ionics 262 （2014） 407-410.
・鷲見 裕史、燃料電池、16-1 （2016） 69-73.