全固体電池の研究開発に貢献 固体電解質内イオン伝導度を解析する新手法“ランダムウォーク法”

近年、温室効果ガスの排出を全体としてゼロにする脱炭素(カーボンニュートラル)への取り組みが世界で進んでいます。その実現に大きく貢献すると期待される次世代電池の一つに全固体電池があります。全固体電池はその高いエネルギー密度や安全性・短い充電時間など、さまざまな面で優位性を持つ二次電池であり、国内外で高性能化に向けた研究開発が盛んに行われています。電池の高性能化のためには、電池の内部を定量的に評価する必要があります。全固体電池の研究開発においては、固体電解質内のイオン伝導度(イオンが電気を運ぶ能力のこと。伝導度が高いほうが高性能)の評価が必要です。

本稿では、全固体電池の固体電解質内におけるイオン伝導度を評価する新たな解析手法であるランダムウォーク法¹⁾、およびその新手法を実現する、東陽テクニカが開発したソフトウェア「Z-RW-Analysis」についてご紹介いたします。

1)国立研究開発法人新エネルギー・産業技術総合開発機構(NEDO)委託業務における国立大学法人東京大学の研究開発成果[1]

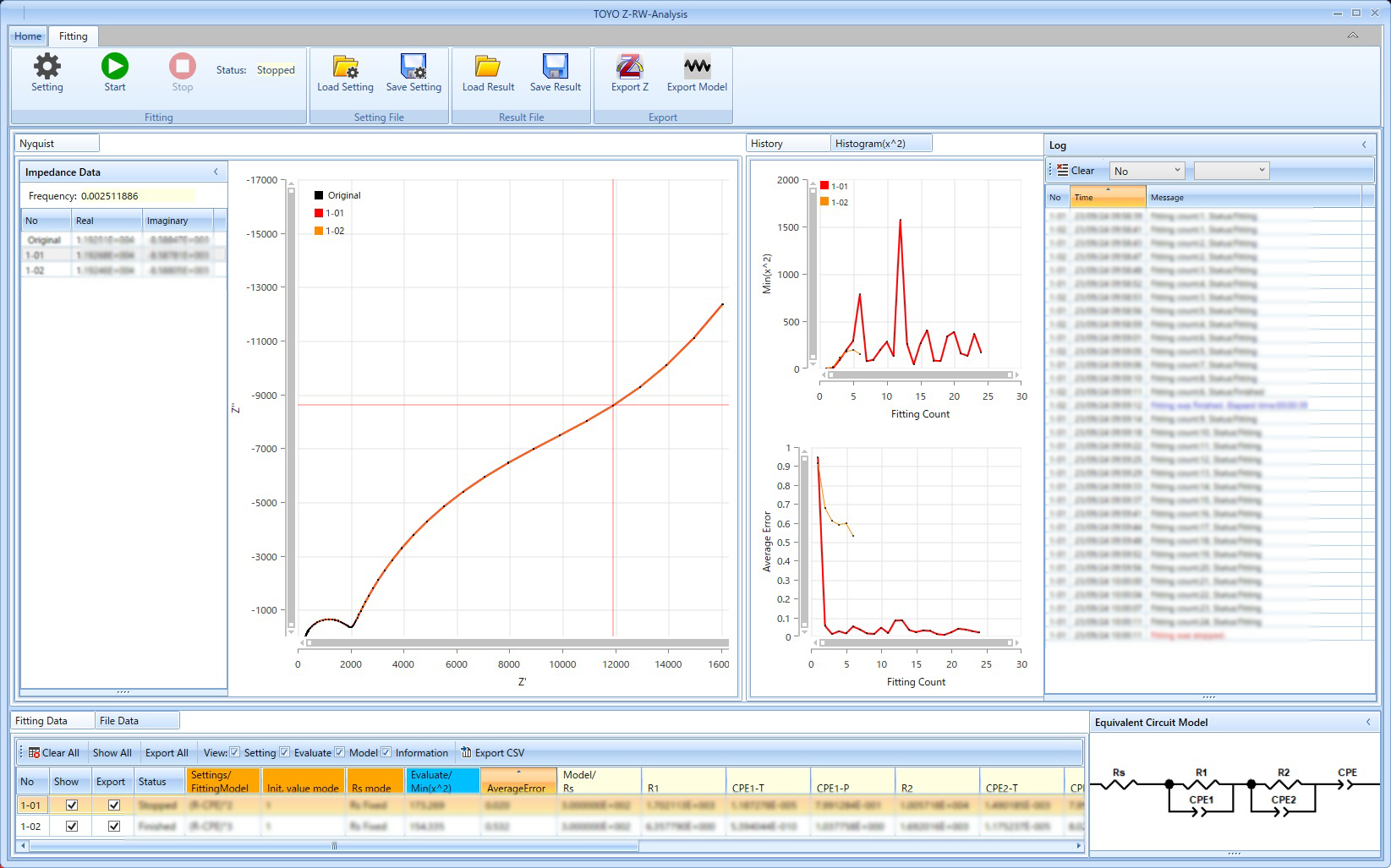
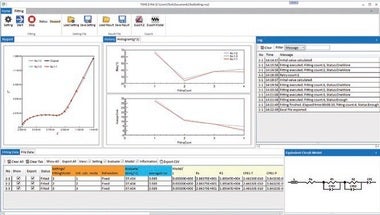
「Z-RW-Analysis」の画面

電気化学インピーダンス分光法(EIS)とは

電池内部の反応現象を非破壊で定量的に評価する手法の一つとして、電気化学インピーダンス分光法(EIS)があります。一般的には電池などの試料に対して微小な交流電圧を加え、その際の電流の応答を測定することにより、交流インピーダンス(電流の流れにくさ)を測定するという手法です。EISで得られたデータは、周波数に対する電気化学的な挙動を示すスペクトルを、複素平面プロット(ナイキストプロット)で表現できます。

固体電解質に対するEISと等価回路フィッティング

物質が電気を通しやすいか否かの指標として電気伝導度(導電率、抵抗成分の反比例値)が用いられます。固体電解質は、内部でイオンが動くことにより電気伝導性(イオン伝導性)を示す点に特徴があります。例えば、全固体リチウムイオン電池(LiB)であれば活物質であるリチウムイオンのイオン伝導度を評価することが重要となります。

固体電解質の両端の電極間におけるイオン伝導は、①粒内(バルク)におけるイオン伝導、②粒界におけるイオン伝導、③電極反応の三つの過程からなることが知られています。

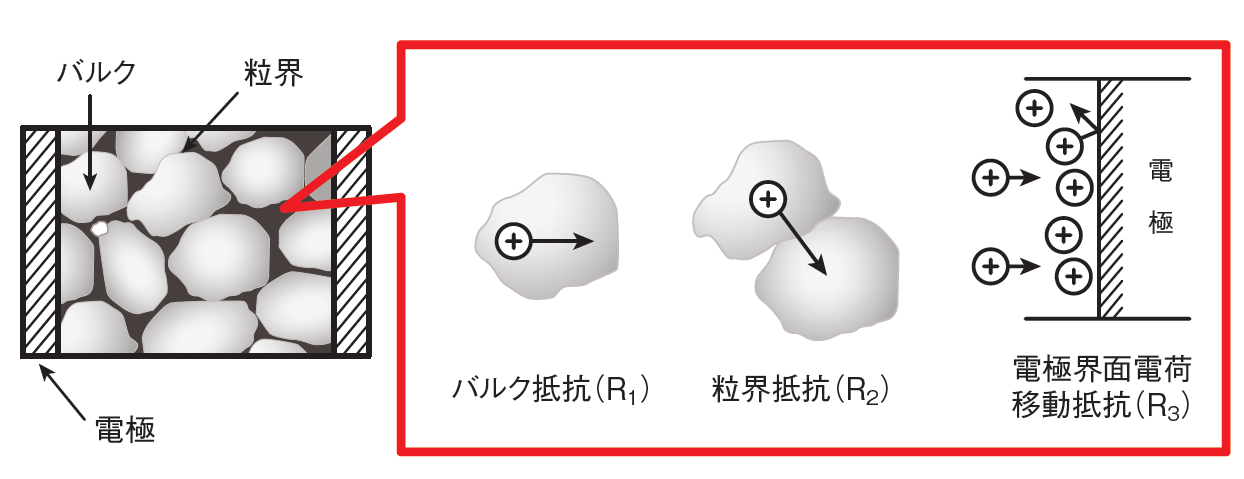
図1：多結晶固体電解質のイメージ

これらの各過程のインピーダンスを等価回路で表現する場合、各過程の反応抵抗成分は直列に接続されていると見なせるため、図2のようになります。

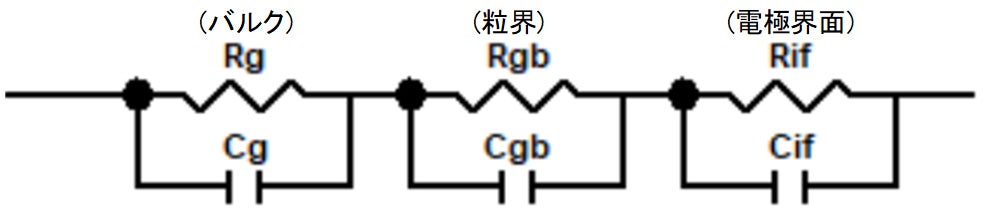
図2：固体電解質のインピーダンス等価回路モデル例

図2に示す等価回路の典型的なナイキストプロットを示すのが図3です。一般的に、固体電解質のインピーダンス等価回路を構成する各過程の緩和時間は、①バルクにおけるイオン伝導、②粒界におけるイオン伝導、③電極反応の順に長くなります。そのため、図3に見られる三つの半円は、高周波領域(図の左側)から上記の各緩和時間順の過程に対応します[2]。

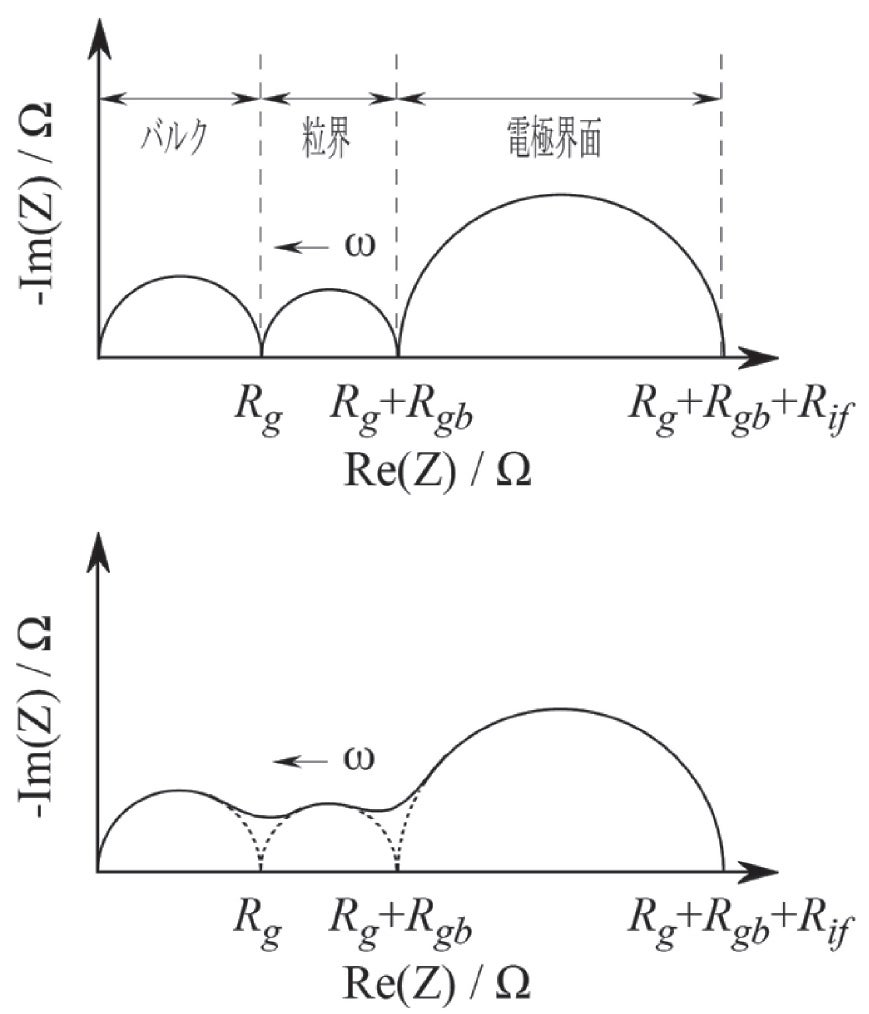
図3：固体電解質のインピーダンスナイキストプロット例

「最急降下法」の課題

等価回路フィッティングの計算手法(非線形最小二乗法のアルゴリズム)の一つとして最急降下法(SD法)があります。ただし、このSD法には「初期値によっては、その解が極小値に陥る場合がある(大域的最適解に達せず局所的最小値に留まる)」という課題があります。

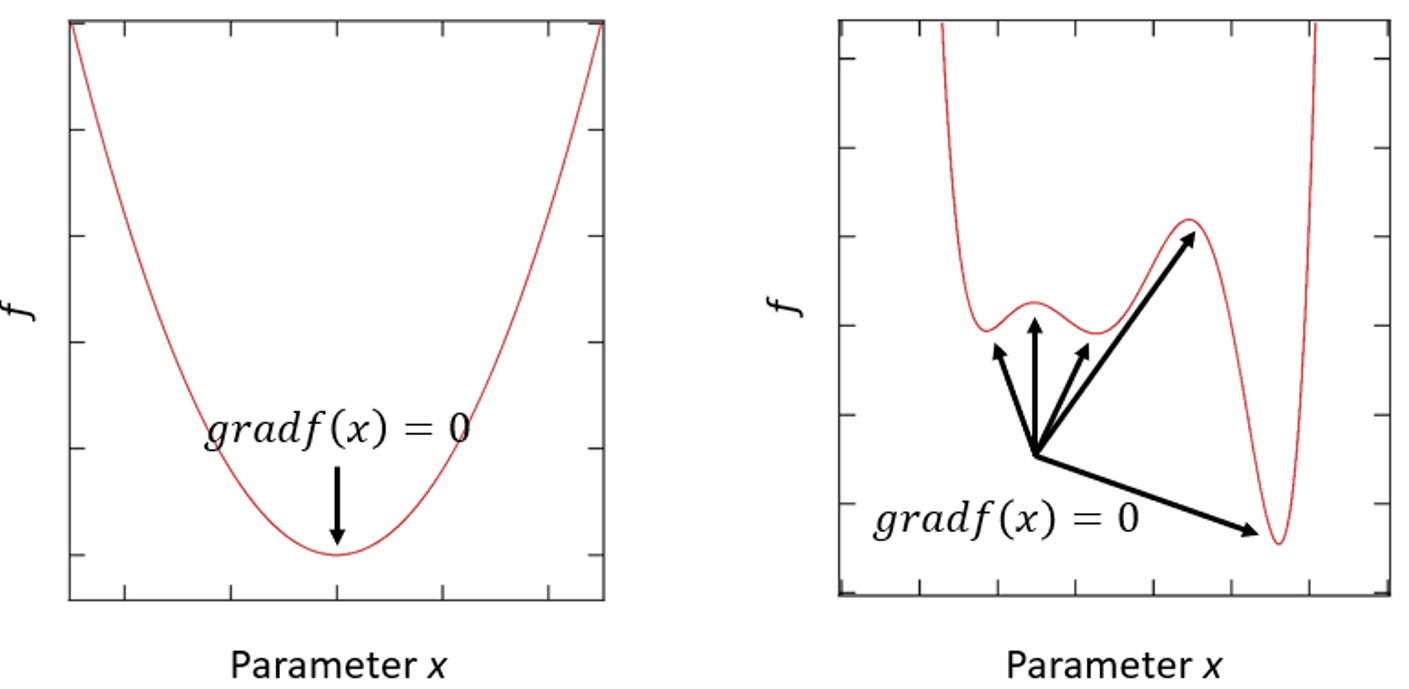
図4:左：極小値が1つならば結果は初期値に依存しない
右：多数の極小がある場合、結果は初期値に依存

つまり、フィッティング結果が初期値に大きく依存してしまうという課題です²⁾。

2)東陽テクニカで長年取り扱っている米国Scribner Associates社製等価回路解析ソフトウェア「ZView」では、等価回路フィッティングの計算手法として、レーベンバーグ・マルカート法(LM法)が適用されている[4-5]。LM法は、ガウス・ニュートン法(GN法)とSD法を内挿した手法と言えるが、LM法はGN法よりもロバストであり、初期値が解から大きく外れる場合でも解けることが多い。またLM法で用いられる減衰係数λは反復計算毎に調整されるが、λが大きい場合(解から離れている場合)にはLM法はSD法に近くなる。よってLM法はSD法と比較すれば初期値に対する依存性は低く局所最小値に陥る確率も低いとされているが、確実性をより高める為にはより良い初期値の適用が重要と言える。

新手法「ランダムウォーク法」による課題解決

全固体電池の固体電解質EISデータには、高周波域にて時定数を持つ(つまり緩和時間が短い)複数の反応抵抗成分が含まれ、さらにはイオン拡散成分が低周波域まで広がっているケースがあります。このような場合、等価回路フィッティングの難易度が上がります。東京大学総合研究機構 幾原研究室の川原一晃助教は、2018年のNEDO委託研究成果として上記課題を解決する新たな解析手法を発表されました[1]。この論文では、主に以下2点について論じられています。

1.MCMCの一つであるランダムウォークM-H(メトロポリス-ヘイスティングス)法により、固体電解質EISデータに対する各過程のイオン伝導度を分離・同定する手法
2.実試料に対する検証結果

ここでMCMC法(マルコフ連鎖モンテカルロ法)とは、ベイズ統計学の近似推論手法群のことであり、“事前分布”と“尤度分布”から(ベイズの定理における)“事後分布”を導出するアルゴリズム群の総称で、機械学習の分野などでも利用されています。ランダムウォークM-H法(本稿では“RW法”と記載)は、MCMCを実現するアルゴリズムの一種になります。

図5にRW法の計算フローチャートを示します。RW法では、極小値(局所解)を導出後も、より最適な極小値を探索し続けます。そのため、(原理的には)初期値に依らず最適な極小値(最適近似解)を得ることが可能です。またSD法のように導関数を計算する必要もなく、よりシンプルなアルゴリズムとなっています。

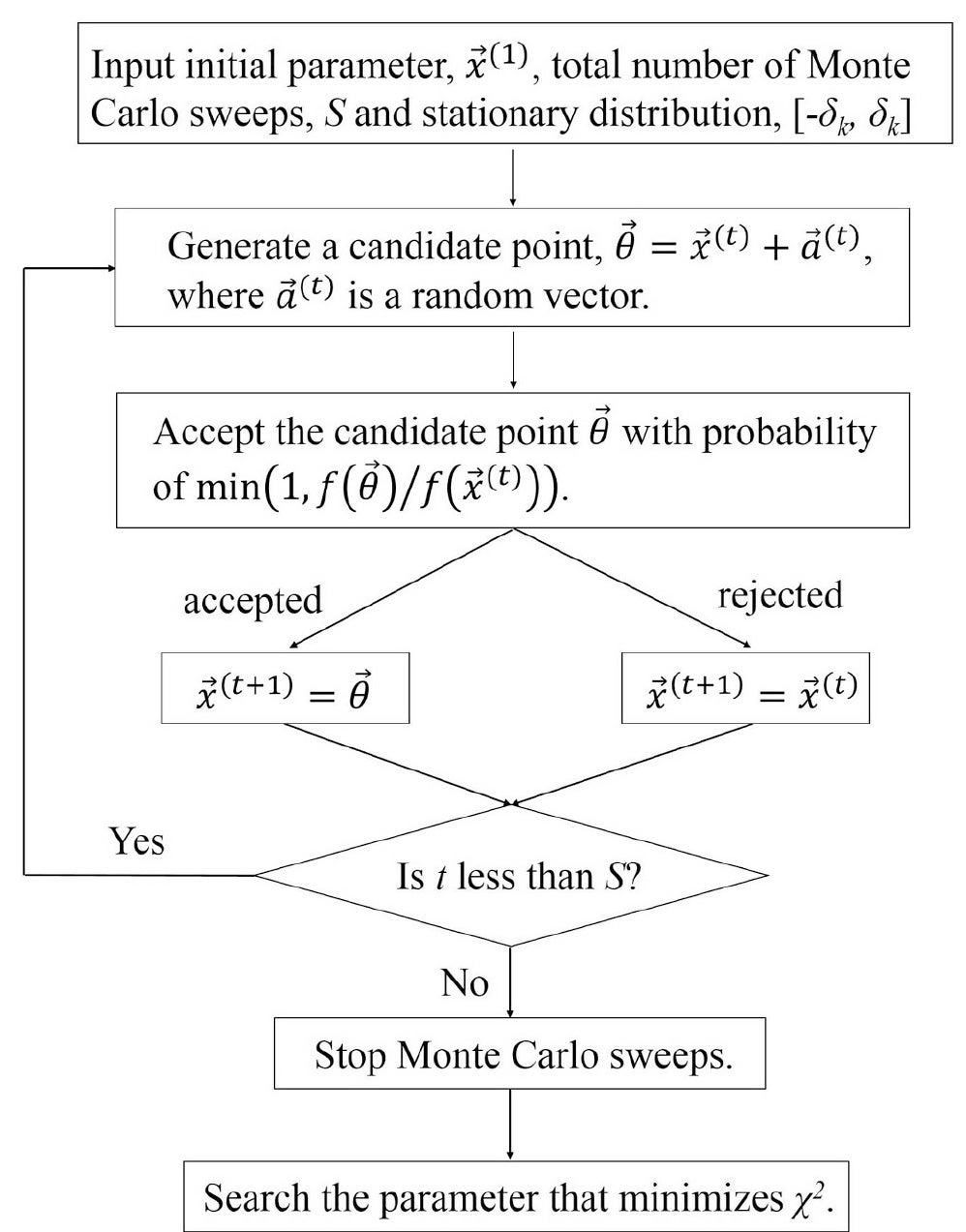
図5：RW法によるEISデータのフィッティング処理フローチャート

SD法とRW法の初期値依存度の比較

図6-1に酸化物系固体電解質の等価回路モデル、図6-2にEIS測定データに対する3パターンの初期値①I₁,②I₂,③I₃におけるSD法とRW法の各等価回路フィッティング結果をそれぞれ示します。

SD法の場合、測定データと値が近い初期値①では、測定データとフィッティング結果が重なっています。しかしながら、値が離れている初期値②・③ではフィッティング結果にも違いが見られます。

一方でRW法の場合、いずれの初期値でも同じフィッティング結果が得られ、元の測定データとも重なっていることが分かります。このように、SD法ではフィッティング結果が異なってしまうような初期値においても、RW法では最適解を得ることができることが分かります。

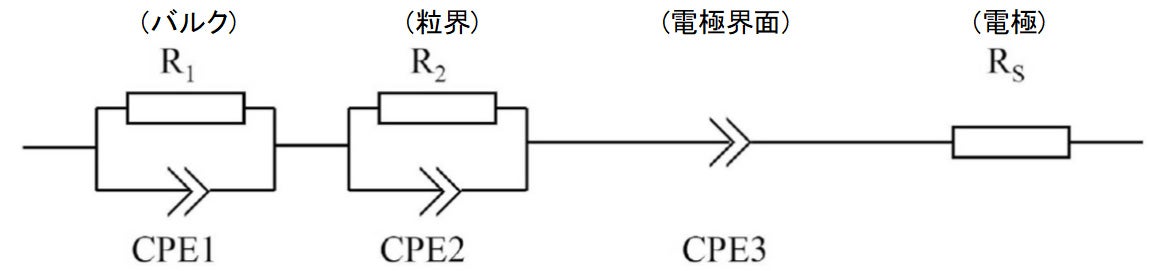
図6-1：酸化物系固体電解質の等価回路モデル

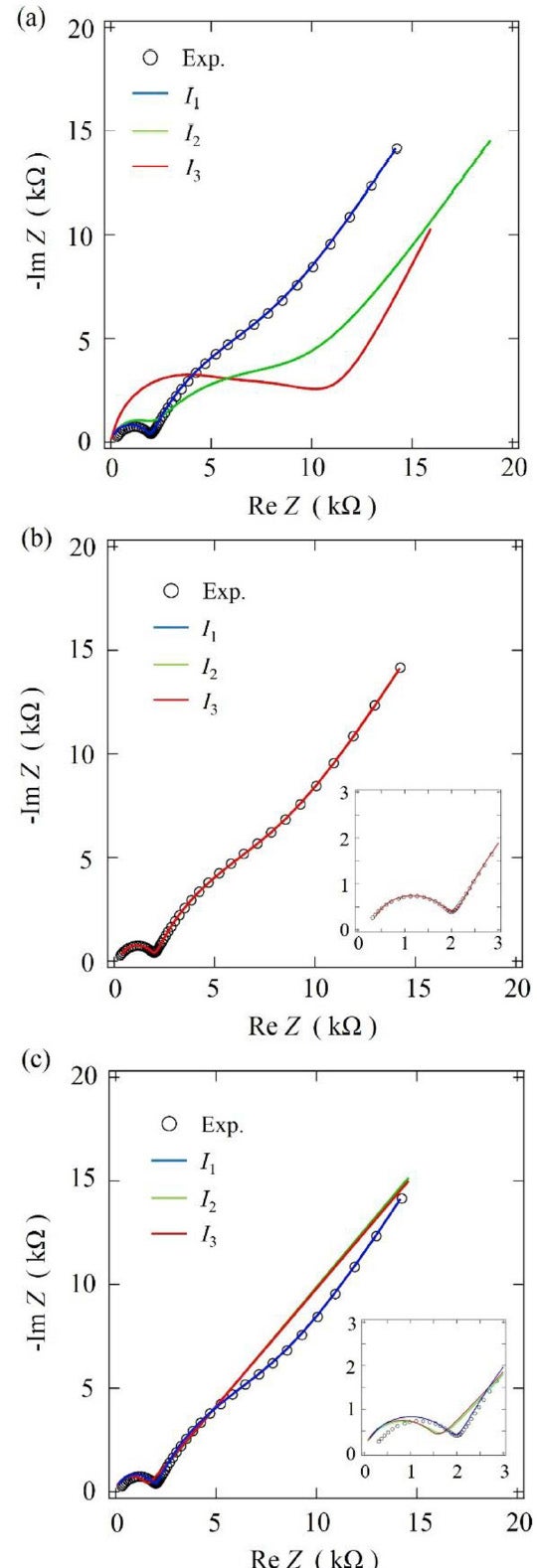
図6-2:測定データとフィッティング結果データの比較
黒点：測定データ(フィッティング前データ)
(a) グラフ：初期値(フィッティング前)
(b) グラフ：RW法フィッティング結果(初期値による差異なし)
(c) グラフ：SD法フィッティング結果(初期値による差異あり)

自社開発ソフトウェア「Z-RW-Analysis」

当社では、RW法によるEISデータ等価回路フィッティング解析を実現する自社製ソフトウェア「Z-RW-Analysis」(Z-RW)を新たに開発し、2023年10月より販売を開始しました。

【「Z-RW-Analysis」の特長】

■ 複数設定パターンの同時解析
■ フィッティング解析で用いる初期値の自動算出機能
■ 初期値に依存しない高いフィッティング精度
■ 解析結果の等価回路モデルデータをScribner Associates社製等価回路解析ソフトウェア「ZView」に出力
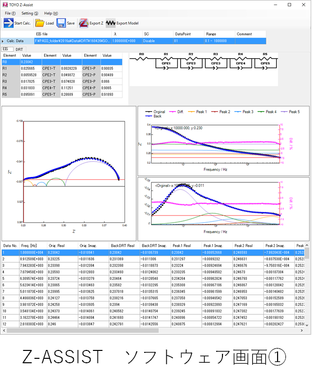
■ 自社開発インピーダンス解析支援ソフトウェア「Z-ASSIST」による緩和時間(DRT)解析[6]で得られた時定数情報を初期値として反映可能

前述の通り、RW法はSD法などの勾配法と比較し、その初期値依存性は(原理的には)より低いアルゴリズムです。しかしながら実際の解析現場では、解析時間やPC処理性能は限定されますので、より良い初期値を設定することは計算時間短縮に効果的です。「Z-RW-Analysis」ではこれらの点に関し独自の工夫を加えています。

「Z-RW-Analysis」の今後の拡張性

本製品を固体電解質用としている理由は、現状対応する等価回路モデルが固体電解質の典型モデルのみのためです。今後の機能追加により他の等価回路モデルにも対応することによって、その用途を技術的には拡張可能です。

参考文献

[1] “Unique fitting of electrochemical impedance spectra by random walk Metropolis Hastings algorithm”
(Kazuaki Kawahara, Ryo Ishikawa, Yuichi Ikuhara et al., Journal of Power Sources 403(2018) 184-191)
[2] チュートリアル電気化学測定法 第9シリーズ
『固体電解質の基礎と測定法1』　(雨澤浩史)
[3] 『固体電解質における交流インピーダンス測定について』
(国立大学法人東京農工大学 重原淳孝名誉教授)
[4] ZView 4.0 Operating Manual: “ZView Equivalent Circuits is based on the LEVM 6.0 program written by Dr. J. Ross Macdonald.”
[5] Levenberg-Marquardt algorithm: J. J. More in G. A. Watson (ed.), Lecture Notes in Mathematics: Vol. 630, Numerical Analysis, Springer-Verlag, Berlin, 1978, pp. 105-116.
[6] 東陽テクニカルマガジン22号2016.11技術解説『緩和時間分布解析法の基本原理』　(平野隆行) https://www.toyo.co.jp/magazine/detail/id=34131