ナノインデンテーションによるひずみ速度感受性試験
はじめに

金属材料は変形時の速さ、すなわちひずみ速度によりその応力-ひずみ関係が変化します。 ひずみ速度感受性(SRS)は材料のクリープ傾向を定量化するために重要な材料特性です。はんだなどにおいては疲労寿命の予測パラメータとしても用いられます。
基本的にクリープしない材料ではひずみ速度感受性は0となり、ひずみ速度感受性の高い材料については値が大きくなります。ひずみ速度感受性が高い材料においては、十分に低いひずみ速度でも、小さな応力で塑性変形を引き起こす可能性があります。本ページでは、熱ドリフトの影響を抑えた薄膜や微小域のひずみ測定感受性評価を行うための新しい手法を提案します1,2。
シリコン上に堆積したCu薄膜およびNi薄膜のひずみ速度感受性を測定するために本手法を用いています。その結果を同等の材料について公表値と比較しています。Maierらは、超微細粒Niのひずみ速度感受性をナノインデンターにより0.019と測定し、この値をNiについて公表されている単軸引張試験によるひずみ速度感受性試験の結果0.0163と比較しました。またYeらはCuに関して同様の測定方法を用いることで、粒度の関数として報告しています4。100nm~1500nmのオーダの結晶粒度に対して、Cuのひずみ速度感受性指数の値は0.005~0.02の間で変化しました。本手法で得られたこれらの値(Niでは0.016~0.019、Cuでは0.005~0.02)は、今後の研究に期待が集まります。
理論
伝統的なクリープ試験(単軸引張試験)では、塑性応力 σ とひずみ速度 ε' の関係は次式で表されます

ここで、 B* は定数であり、 m はひずみ速度感受性指数です。
なおひずみ速度感受性指数 m は常にゼロ以上となります。ひずみ速度感受性が無視できることが明らかな材料では、 m はゼロに近い値となり、 σ は一定となります(サファイアはそのような材料の一例)。ひずみ速度感受性が高い材料ほど、 m は大きな値となります。 また硬さ H が塑性応力 σ に直接関係する場合、硬さも同様の現象を示すことが知られており、次の関係式が得られます。

?式において B は定数であり(ただし?式のB*とは異なる)、 ε' は荷重を荷重速度で割った値、 (P'/P)1 として定義される押し込みひずみ速度です。ひずみ速度感受性指数 m は、?式と?式で同じ値を持ちます。?式の両辺の対数をとり、簡略化すると次のようになります。
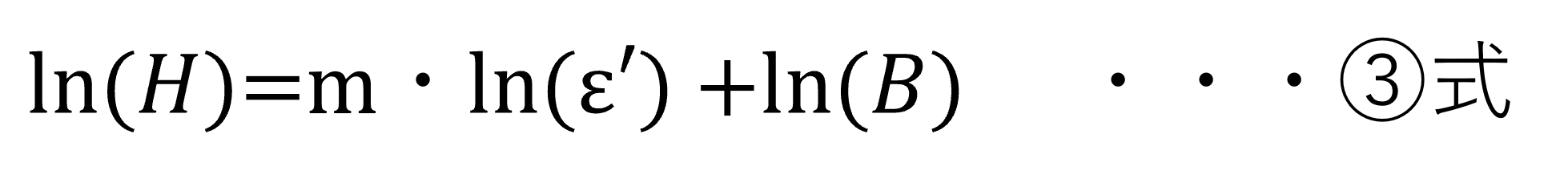
多くの材料に関して硬さの対数とひずみ速度の対数はリニアな関係があり、その傾きがひずみ速度感受性指数 m となります。そしてひずみ速度感受性指数を決定するためには、ひずみ速度の一定以上の範囲にわたり硬さを測定する必要があります。しかし、温度変化による熱ドリフトの影響は装置並びに試験サンプルの自然な膨張/収縮を引き起こします。測定時間が長いほど熱ドリフトの影響は大きいため、特に低ひずみ速度での硬さ測定値に悪影響を及ぼします。
問題点をわかりやすくするために具体例を示します。ε'=0.002/secのひずみ速度で250nmの押し込み深さにおけるNiの硬さを測定します。このひずみ速度の場合、250nmの押し込み深さに達するのに約1200秒(20分)を要します。これは熱ドリフトの速度が1Å/secであったとしても、熱ドリフトによる変位が目標変位(250nm)の120nm(約50%)と高い可能性があることを意味します。さらに、材料がクリープするため、単に荷重を一定に保持して変位を測定するだけでは熱ドリフトを測定することはできません。そのため、低ひずみ速度で硬さを測定するためには、熱ドリフトの問題を注意深く考慮する必要があります。
多くの金属では、弾性係数はひずみ速度に依存しません。これは、Niについて実験的に実証されています3,5。これが真であれば、インデンテーション試験で高ひずみ速度における弾性率を測定することができることになります。そして次に、測定された弾性剛性と既知の弾性率の関数として他のひずみ速度における接触面積を計算することができます。そうすることで直接変位を測定せずに試験することができます。これが本研究で取られたアプローチです1。
なお厳密に言えば、「押し込みひずみ速度」という用語は、変位速度を変位で割ったもの 「h'/h」 を指します。しかし、硬さの定義から考えると、 h'/h≈0.5(P'/P) と示すことができます。?式はいずれの定義のひずみ速度についても成り立ちます。 二つの定義の間の定数(0.5)の差が単純に定数 B に吸収されるため、速度は「ひずみ速度」という言葉である 「h'/h」 よりもナノインデンターにおいて流動的に制御が容易な P'/P を使用します。 特に記載がない限り、本ページではひずみ速度は 「P'/P」 を指します。
試験サンプルの弾性係数 E が既知であれば、接触面積 A は測定された剛性 S から直接計算できます。インデンテーション試験のデータを解釈するために一般的に表現7,8するために、Sneddonの剛性方程式6から始めます。

ここで、Erは複合弾性率です。試料と圧子の弾性率とポアソン比から、次のように結びつきます。
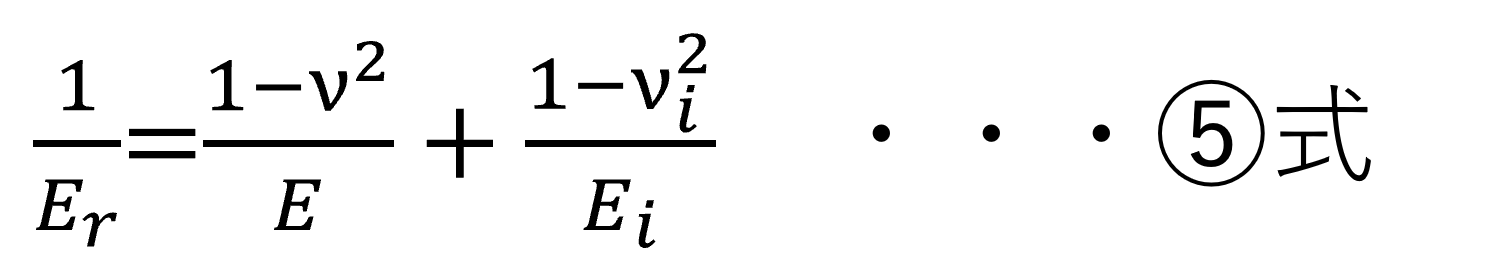
AEを算出するために④式を整理します。

面積が弾性率の関数として計算されることを伝えるために、ここでは面積の表記をAEとします。
硬さは、荷重を接触面積で割ったものとして計算されます。

さらに、⑥式により計算された面積を用いて、面積関数から変位を求めることができます1。面積関数が接触深さhcの2次関数として考えると容易に表すことができます。
※面積関数がA=mohc2+m1hcの形式を持つ場合、接触深さは⑧式で表されます。
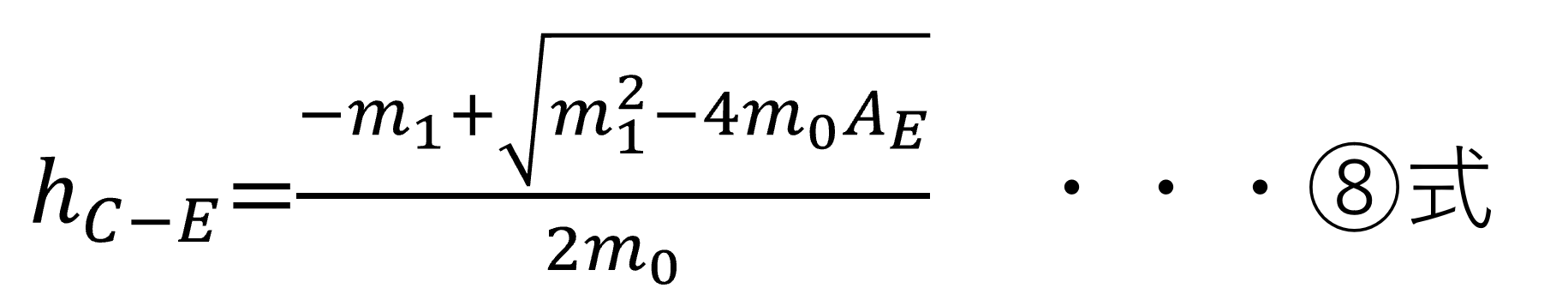
最後に、変位は次のように計算されます。
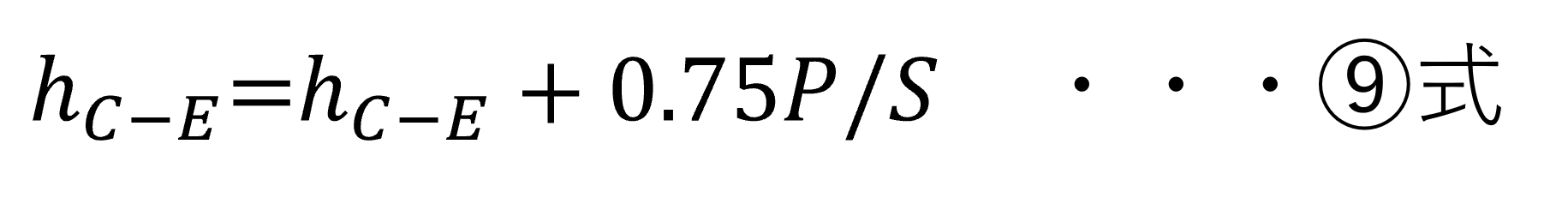
ここで、Pは押し込み荷重です。
要約すると、低ひずみ速度における熱ドリフトは変位の測定値に影響を及ぼすため、弾性率と接触剛性の関数として間接的に接触面積を計算します(⑥式)。これは、弾性率がひずみ速度に依存しない限り有効です。
この間接的な決定法を用いて硬さと変位の両方を計算しています。
これらのパラメータが弾性率の関数として得られたものと判別するために、面積関数、硬さおよび変位をAE、HE、およびhEと表記します。
試験手順
サンプル
本研究では、溶融石英、サファイア、シリコン上のCu膜およびNi膜の4つの試料を試験しました。溶融石英とサファイアは、本手法の評価のためであり、2種類の金属膜が実際に評価を行うサンプルです。
CuとNi膜は室温でDCマグネトロンスパッタリングによりSi基板上に蒸着しました。チャンバーのベース圧力は、 6×10-6 Paであり、CuおよびNi膜はいずれも高密度な(111)面構造になっています。Cu膜でのみ平均間隔~20nmの高密度ナノスケール双晶構造が観察されました。
試験装置
KLA社製Nano Indenter®システムを試験バーコビッチ圧子を用いて試験を行いました。押し込み深さの連続的な関数として硬さと弾性係数を測定するために、連続剛性測定(CSM)オプションも使用しました9。
試験方法
この試験では、従来の押し込み試験と新しい本手法の2つの試験方法を用いる必要があります。最初に従来の押し込み試験法で、4サンプルすべての硬さおよび弾性率を測定しました9(この試験方法は、⑥~?式で説明した解析を採用していません)。各試料ひずみ速度 0.05/sec、最大深さ500nmという条件で12点押し込み試験を行いました。溶融石英とサファイアについては、400nmの押し込み深さにおける特性を使用し、薄膜金属については膜厚の20%に相当する押し込み深さの特性を使用しました。
次に、Accufilm法(基材の影響を補正する機能)を用いて、ひずみ速度の関数として硬さを評価しました。この方法は、⑥~⑨式に従って接触面積、硬さ、接触深さ、および変位を自動的に計算します。なおこれらの計算に使用した弾性率は、最初の測定結果から得られている値です1。各試料について、3つの異なるひずみ速度において12点ずつ押し込み試験を行い、溶融石英については同様の試験を2サイクル実施しました。
結果
弾性係数の値を用いて、低ひずみ速度での試験では?式に従い面積、硬さ、および変位を計算します。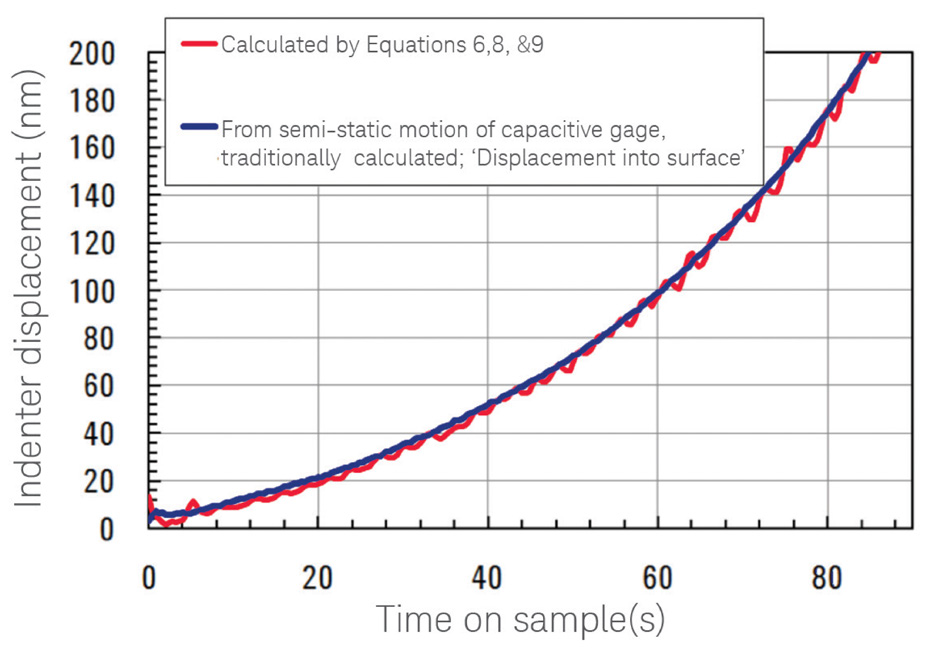
図1. Accufilm法を用いて、ε'=0.05/secで試験したNi膜の押し込み試験に対して2つの方法で決定した変位。
青色はキャパシタンスゲージの準静的動作に由来。赤色は押し込み試験法で求めた弾性率(224.1GPa)を仮定して計算。
図1は、変位を測定するために本研究で提案した2つの方法を比較したものです。それぞれのトレースは、いずれもε'=0.05/秒でのAccufilm法を用いたNi膜の試験データです。青色のトレースは、変位を測定するキャパシタンスゲージの出力に由来した変位量であり、赤色のトレースは、弾性率を224GPaに設定して、⑥、⑧、?式から得ています。赤色のトレースはずっと「ノイズが高い」ものの、2つのトレースは試験全体を通して非常に近い結果です。
図2は、図1と同じ試験ですが、硬さを得る2つの計算方法を比較しています。青色のトレースは、荷重、変位、および剛性を測定する方法に従来の押し込み試験の解析を適用して得ています。赤色のトレースは、モジュラスを224GPaに仮定し、⑥~?式を適用することによって得ています。このひずみ速度(ε'=0.05/sec)では、青色のトレースが明らかに優れていますが、赤色のトレースは熱ドリフトに対する影響がないという長所を担っているため、低ひずみ速度試験においては適しています。
※膜厚の約20%付近のハイライトされたデータを平均として、この試験について硬さの値を使用しています。
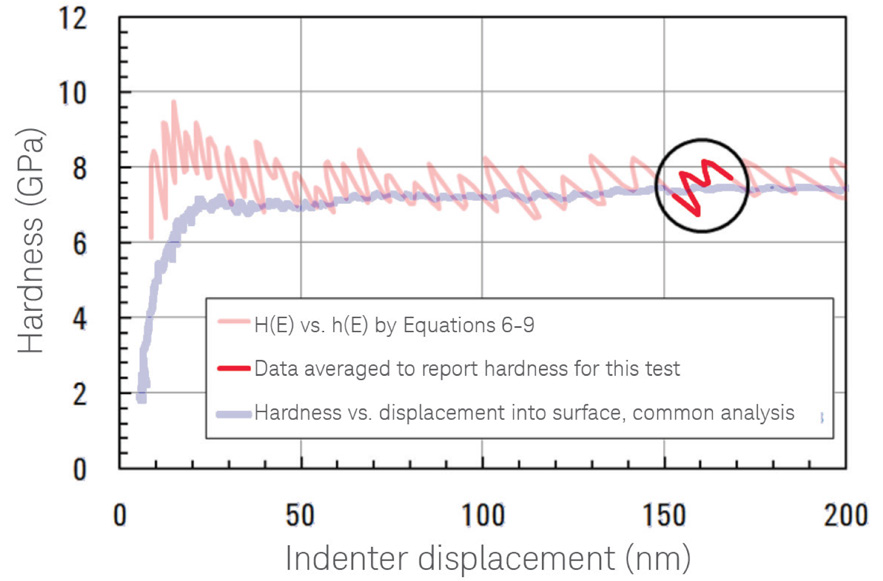
図2. GシリーズXP Thin Film SRSメソッドを用いて、ε'=0.05/secで試験したNi膜の押し込み試験について2つの方法で求めた硬さ。青色のトレースは、CSMデータの標準的な解析から計算。赤色トレースは一定の弾性率を仮定して計算しており、その値は h=160nm(膜厚の20%) におけるインデンテーション試験の結果 224.1GPa でである。膜厚の約20%付近のハイライトされた箇所のデータを平均化して硬さを報告。
図3は、本分析の利点を示しています。この図は、Accufilm法を用いてε'=0.01/secでNiに対して実施した12試験すべてを示しています。このひずみ速度はスタンダードテスト(ε'=0.05/sec)で用いるひずみ速度より5倍遅いことに注意が必要。本試験における硬さ(青)のばらつきは、熱ドリフトによるものであり、新しい手法による硬さ(赤)は、ノイズは増えますがより正確です。
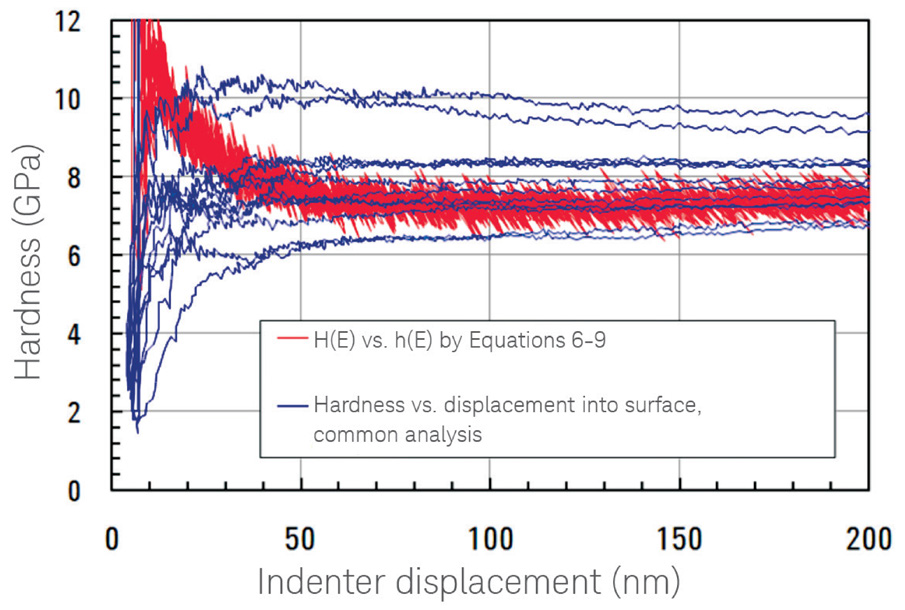
図3. Accufilm法を用いて、ε'=0.01/secで行ったニッケル膜上の全12試験について2通りの方法で求めた硬さ。青色のトレースはCSMデータの一般的な分析から計算。赤色のトレースは、弾性率:224GPaを仮定して⑥~?式から取得。赤色のトレースは「ノイズが多い」ものの、熱ドリフトに対する感受性は低く、低ひずみ速度ではより正確。
図4~7は、それぞれのサンプルに関して36(各12点×3条件)点試験した結果をln(HE)対ln(ε')で示しています。これらのプロットでは、1つのデータ点が1つの押し込みテストに対応しています。例えば、図2のハイライトされたデータを平均し、ε'=0.05/秒におけるNiの1試験での硬さ HE=7.579GPa が得られました。
この結果は、(ln(ε'),ln(HE)) = (-2.996,2.025)の位置にある図7に赤色でプロットされた点と対応しています。ひずみ速度感受性指数は、36点の各セットに対する線形の傾きから得ることができ、Microsoft®Excel®のLINEST関数で、この傾きにおける標準誤差も計算できます。これをひずみ速度感受性の不確かさとしています。
次に図4にサファイアの結果を示します。
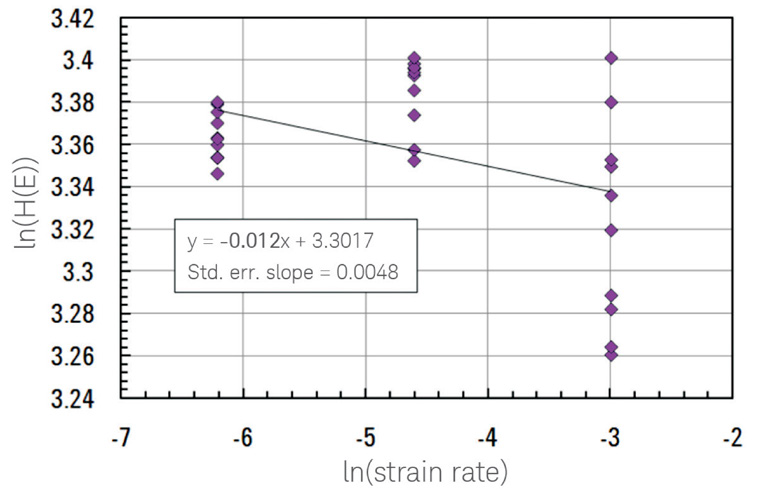
図4. サファイアにおける3つのひずみ速度(各々12点)に対するln(HE)対ln(ε')。予想通り、ゼロに近いひずみ速度感受性の結果となった。線形フィッティングによる傾きは負(m=-0.012)であり、この値の大きさは標準誤差(0.005)と比べてあまり大きくない。
これらのデータに線形フィッティングを行うと負の傾きとなり、m=-0.012±0.005となります。傾きの値は明らかに誤りですが m 対する理論上の下限はゼロでありサファイアはひずみ速度感受性が無視できるため、これは予期せぬことではありません。パラメータの値が真にゼロである場合、そのパラメータの実験的測定値は、わずかに負であることがあります。測定値の大きさが不確かさの大きさと同程度であることから、そのように推測されます。
図5は、溶融シリカに関する2つのサイクル(36点×2セット)の結果を示しています。驚くことにわずかではありますが、この材料の有意なひずみ速度感受性を見出しました。
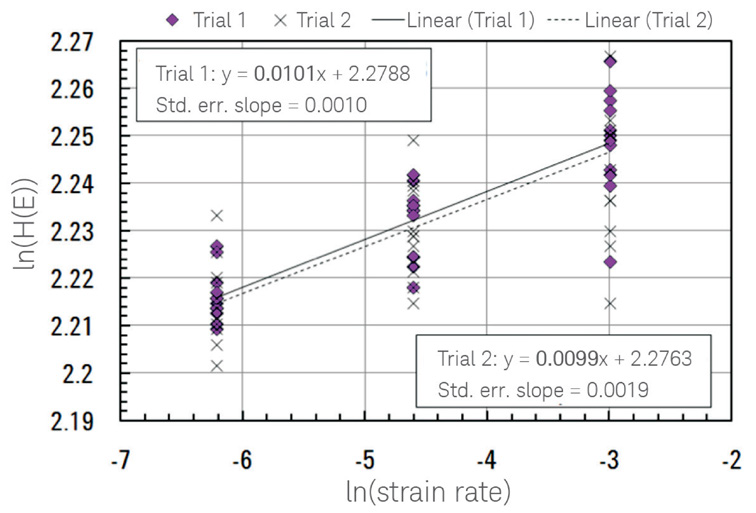
図5. 溶融石英に関しては2セットの試験を実施し、各3つのひずみ速度条件(各12点)に対するln(HE)対ln(ε')。
驚くことに、わずかながら溶融石英のひずみ速度感受性が表れた。
試験サイクル1 : m=0.0101±0.0010 試験サイクル2 : m=0.0099±0.0019。
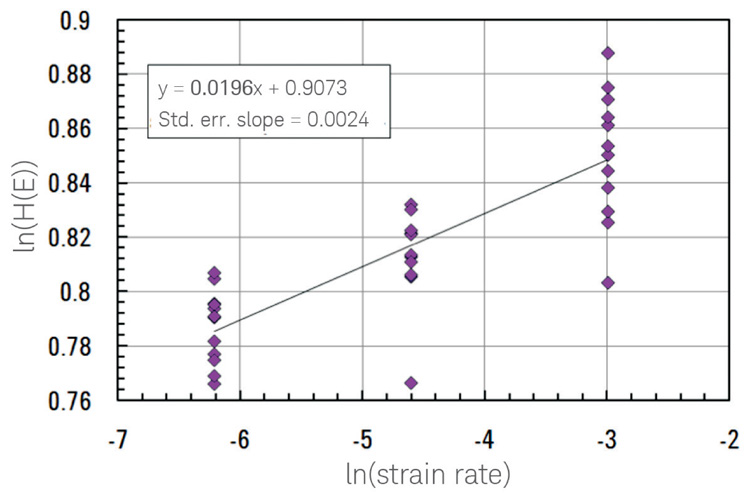
図6. (111)面Cu薄膜(t=1500nm)の3つのひずみ速度条件で12点の試験結果についてのln(HE)対ln(ε')。
ひずみ速度感受性はCuに対して妥当であった。
m=0.0196±0.0024。
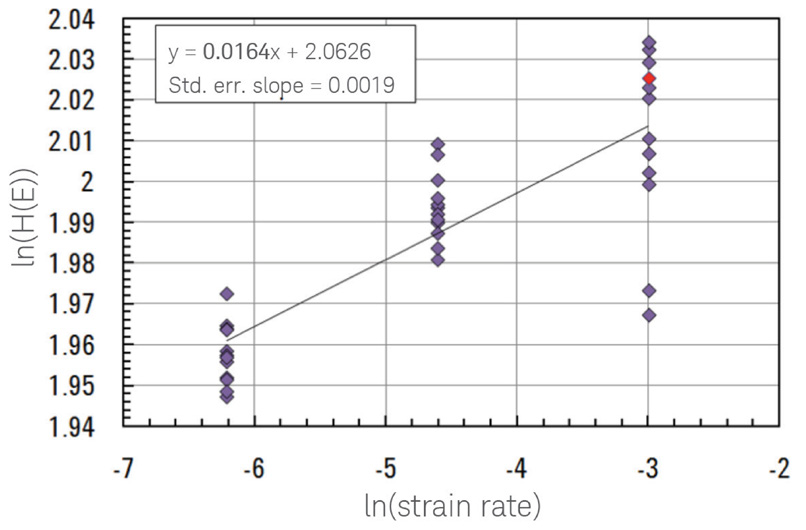
図7. (111)面Ni薄膜(t=800nm)上の3つのひずみ速度で12点の試験結果についてのln(HE)対ln(ε')。
ひずみ速度感受性はNiに対して妥当であった。
m=0.0164±0.0019 ※赤い点は、図2の強調表示されたデータを表します。
図6にCu膜の結果、図7にNi膜結果を示します。 CuおよびNi膜で得られたひずみ速度感受性はこれらの材料に対して期待した値を得ることができました。
考察
本手法では薄膜のひずみ速度感受性を決定するために材料の弾性係数を知る必要があります。しかし、従来の押し込み法によって測定した弾性係数の値はNiおよびCu膜では高い値になっています。Niについては、測定した弾性率(224GPa)は公称弾性率(200GPa)より約12%高く、Cuでは測定した弾性率(153GPa)は公称弾性率(110~130GPa)より少なくとも18%高いです。これらの誤差の原因とこの誤差がひずみ速度感受性の決定にどの程度影響するか?検討する必要があります。
CuとNiの弾性率の測定値が高くでる原因は以下が考えられます。まずNiの弾性率はパイルアップにより高い値が出ていると考えられます。パイルアップが発生した場合、接触面積の計算に用いられるモデルは真の接触面積を想定するため、接触面積が小さくなり弾性率を過大に予測します。またパイルアップと基板の影響により、Cuの弾性率は高くなったと考えられ、両方とも押し込み深さの増加と共に測定値がより高くなる傾向があります。パイルアップと基板の影響の両方に対処するための測定手法は存在します。例えば、より浅い押込み深さで試験を行うことがや、分析モデルを用いて基質の影響を補正することができます10。
しかし、こうした対策は理想的でも必要でもありません。最終的な目標が、⑥式によって剛性および弾性率の関数として接触面積を計算することである場合、⑥式で使用する必要のある弾性率は、基板の影響下で測定された剛性に対応するものです。しかし、ひずみ速度感受性の測定において重要なことは、硬さの絶対値ではなく、ひずみ速度の変化による硬さの変化であるため、弾性率にあまり敏感ではないことが分かっています。
これを検証するために、130GPaと200GPaの弾性率の値をそれぞれ用いて、CuとNi膜のひずみ速度感受性を計算しました。得られたCu膜のひずみ速度感受性は0.0192±0.0019であり、ni膜のひずみ速度感受性は0.0188±0.0016となりました。つまり弾性率の正確な値は、この方法によって得られるひずみ速度感受性への影響は小さいです。
少なくとも1つのインデンターメーカーが、熱ドリフトの問題に対処するために、デュアルプローブ設計を提供しています。動作原理は、第1の参照プローブが、試料や装置の熱膨張/収縮に追従するために表面を、第2のプローブは押し込み試験を行います。押し込み試験プローブと参照プローブ間における変位の相対差を真の変位としています。しかしながら、このアプローチは、参照プローブの力に応答して材料がクリープする場合は意味がありません。なぜなら2つのプローブ位置の違いが、時間に依存した変形を調べるための応答そのものを除外しているためです。 長い試験時間が興味深い材料は、参照プローブに反応してクリープすると思われる材料です。したがって、参照プローブの設計は、解決策が最も必要とされる、こうしたサンプル(すなわち長時間にわたる弾性材料の変形を観測する場合)に対する熱ドリフトの問題についての解決策として失敗しています。
CSMオプションによる剛性の動的測定は、2点の理由からこの試験における重要な側面をもちます。第一に、この試験では弾性係数の正確な知識が不可欠です。実質的にクリープを示す金属では、除荷曲線が弾性回復とクリープの両方を顕在化するため、除荷曲線の勾配から接触剛性 S を正確に得ることができません。また他方からもう一方をデコンボリュートする実用的な方法はありません。このような材料では、剛性(従って弾性係数)は、CSMオプションによって使用される小さな振動によってのみ正確に測定することができます。第二に、一度弾性係数が分かれば、非常に低ひずみ速度の押し込みに対しても、熱ドリフトに敏感でない硬さ値を正確に決定することができます。
まとめ
KLA社のナノインデンターではCSMを用いたひずみ速度感受性試験を行うことができます。本ページで紹介した試験は熱ドリフトの影響を抑えることができ、ひずみ速度感受性指数に対する不確かさを抑制します。またKLA社ではNanoBlitzやExpress Testといった高速押し込み試験オプションを用いることにより、熱ドリフトの影響を抑えた試験を行うことも可能です。参考文献
- Weihs, T.P. and Pethica, J.B., Monitoring time-dependent deformation in small volumes, Mater. Res. Soc. Symp. Proc. 239, 325-330, 1992.
- Maier, V., Merle, B., Goeken, M., and Durst, K., An improved long-term nanoindentation creep testing approach studying the local deformation processes in nanocrystalline metals at room and elevated temperatures, Journal of Materials Research 28(9), 1177-1188 2013.
- Maier, V., Durst, K., Mueller, J., Backes, B., Hoppel, H., and Goeken, M., Nanoindentation strain rate jump tests for determining the local strain rate sensitivity in nanocrystalline Ni and ultrafine-grained Al, Journal of Materials Research 26(11), 1421-1430, 2011.
- Ye, J.C., Wang, Y.M., Barbee, T.W., and Hamza, A.V., Orientation-dependent hardness and strain rate sensitivity in nanotwin copper, Applied Physics Letters 100(261912), 1-6, 2012.
- Hay, J.L., Maier, V., Durst, K., and Goeken, M., Strain Rate Sensitivity (SRS) of Nickel by Instrumented Indentation, Keysight Technologies, Inc., 2011, Document No: 5990-9434EN.
- Sneddon, I.N., The Relation Between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile, Int. J. Eng. Sci. 3(1), 47-57, 1965.
- Oliver, W.C. and Pharr, G.M., An Improved Technique for Determining Hardness and Elastic-Modulus Using Load and Displacement Sensing Indentation Experiments, Journal of Materials Research 7(6), 1564-1583, 1992.
- Pharr, G.M., Oliver, W.C., and Brotzen, F.R., On the Generality of the Relationship among Contact Stiffness, Contact Area, and Elastic-Modulus during Indentation, Journal of Materials Research 7(3), 613-617, 1992.
- Hay, J.L., Agee, P., and Herbert, E.G., Continuous Stiffness Measurement during Instrumented Indentation Testing, Experimental Techniques 34(3), 86-94, 2010.
- Hay, J.L. and Crawford, B., Measuring Substrate-Independent Modulus of Thin Films, Journal of Materials Research 26(6), 2011.