AD変換の基礎 / 第6回 シグマデルタ型ADコンバーター Part2
ノイズシェーピング
AD変換の基礎 / 第5回で取り上げたように、シグマデルタ型ADコンバーターの動作は、対象の信号に対する大幅なオーバーサンプリングが前提になります。このオーバーサンプリングにより、量子化ノイズが測定対象周波数よりもずっと広い周波数レンジに分布します。この時、特殊な例外を除けば、量子化ノイズの挙動はガウスノイズに近く、サンプリング周波数の帯域内に一様なノイズレベルで現れると考えることができます。一方、AD変換の基礎 / 第3回でも簡単に触れたように、量子化ノイズの総パワーは分布する周波数領域の広さによらず一定に保たれるため、ノイズをより広い帯域に分布させることは、測定対象周波数でのノイズレベルを低減することにつながります。この様子をFigure1 1.a.とFigure1 1.b.に示します。
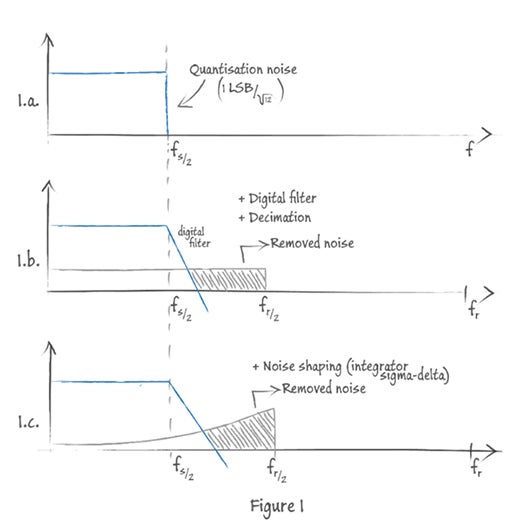
さらに、コンバーター内にある積分器の働きで、ノイズ成分は高周波数領域に偏る事になり、対象周波数でのノイズはより一層低減します。Figure1 1.c.の模式図では、オーバーサンプリングと積分器の両方の働きによって、量子化ノイズが対象周波数外に押しやられる様子を示しています。
2次のシグマデルタADコンバーター
シグマデルタ型ADコンバーターは、シグマデルタ変調と呼ばれる一種のパルス変調を利用した技術です。第5回の例で見ても、レンジに対する入力信号の大きさが“1”パルスの発生頻度に置き換えられていることが分かるでしょう。第5回の例で説明されている変調の仕組みは一次のシグマデルタ変調と呼ばれます。このブロック図に、さらにフィードバックループと積分器を追加した構成は二次のシグマデルタ変調と呼ばれ、高周波数帯域へのノイズの偏り(ノイズシェーピング)がより顕著になります。その結果、量子化ノイズをより低減することができるようになるのです。Figure2は2次のシグマデルタのブロックダイアグラムです。基本的な構造は一次の場合とほとんど変わりありませんが、追加の積分器とそれに付随するフィードバックで拡張されています。
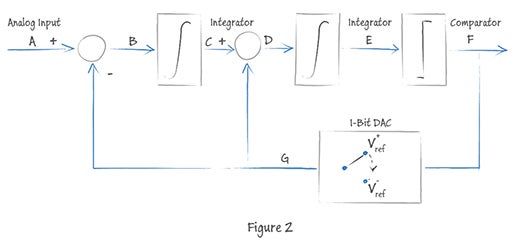
変調の次数を増加させることにより、Figure3のように高い周波数領域へ、より一層ノイズを偏らせることができます。しかし、次数を増やすことは、ハードウェアのコスト増加に直結します。また、本稿では詳しく取り上げませんが、高次になるほど、動作を安定させることが難しくなります。
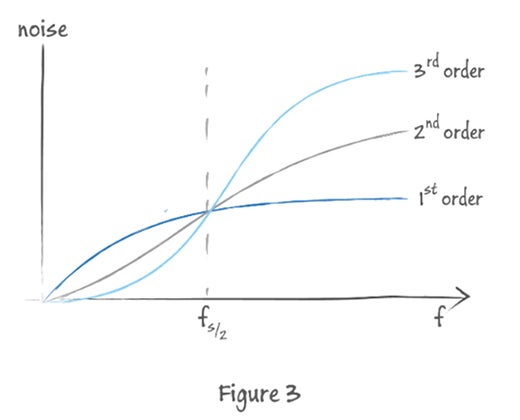
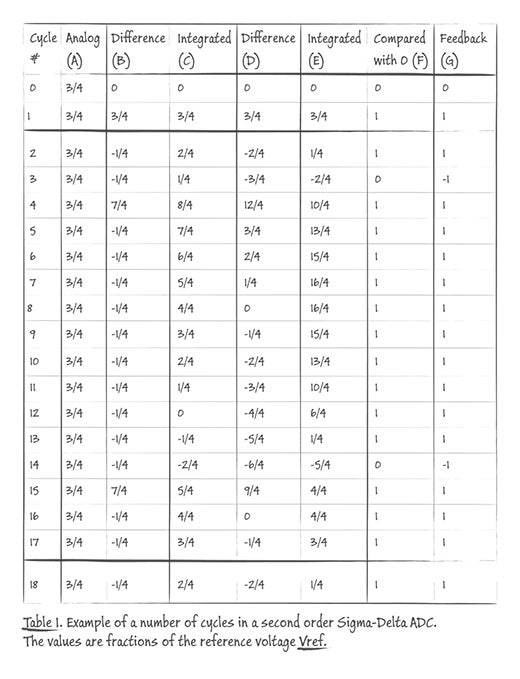
Table1では、AD変換の基礎/第5回と同じく、ステップごとの電圧を表にする事で、2次のシグマデルタ型ADコンバーターの挙動を具体的に説明しています。この例では、一定の入力電圧(3 / 4Vref)が入力される状態を想定しています。 表の見方については、前回を参照してください。
第5回で紹介した一次のコンバーターでは、デジタルの1と0のパターンが8ステップの周期で繰り返され、その周期の中の1/0比率が1 / 4Vrefの整数倍に対応していました。一方、今回の2次構成では、16ステップが1周期になっている事がわかります。
雑記
本稿では、簡単のために1ビットコンバーターに限定して説明していますが、実際には、同じオーバーサンプリングに対してより高いダイナミックレンジを得る事ができるマルチビットコンバーターが一般的です。
こちらもあわせてお読みください。
- 第6回 シグマデルタ型ADコンバーター Part2
- 第5回 デルタシグマAD変換器
- 第4回 測定レンジ
- 第3回 量子化
- 第2回 オーバーサンプリングによるアンチエイリアシング
- 第1回 アンチエイリアシングフィルター