第6回 波動伝播のアクティブコントロール(前編) /
音や振動のアクティブコントロール
安定性の問題とは別に、二次音場および電子コントローラ内の伝播遅延時間は、
「第2回 技術的発達の歴史」で言及したようなシンプルかつ標準的なフィードバック・コントローラの性能を制限する可能性があります。
したがって、有限の波動伝播速度または制御すべき一次音場に関連する遅延時間をそれぞれ利用することが有用であると考えられます。これにより、重ね合わせ点に到達する前に音場で測定することができる場合には時間的な予測が可能になります。
この場合、波動伝播の遅延時間を利用することにより、2次音源の最適な波形を決定することが可能です。図1の原理図から分かるように、波動伝播を本質的に妨げ、あるいは完全に抑制することさえ可能です。
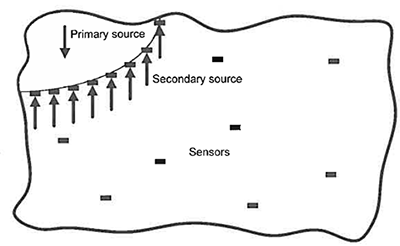
図1 波動伝播のアクティブコントロールの原理図
先行する入射波面から音場を決定することはホイヘンスの原理に由来します。キルヒホッフの法則におけるこの原理は、MalyuzhinetsおよびJesselによって最初に発表された基本的な考察の出発点でした。
この原理によれば、体積Vの外側の外部音源によって生成される体積V内のどのような場でも、体積Vを制限する閉表面S上に分布する代替音源Q*によって等しく生じさせることができます。図2及び図3は体積V内に音の発生源がない場合を示しています。
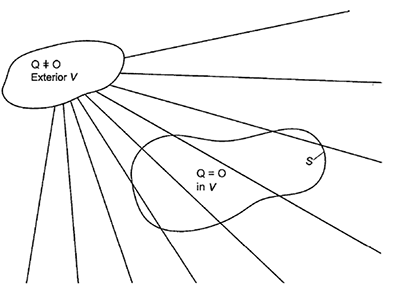
図2 音源Qによるオリジナルの音場分布
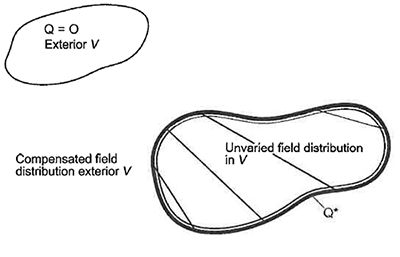
図3 代替音源Q*による音場分布の再現
記号を使った原理からは離れて、これはまさにアクティブコントロールが目指すものです。音源分布の定義-Q*が、図2のように体積V内の所与の場を完全に打ち消し除去するためです。
しかし、この要件は特殊なものではなく、様々な音場分布において満たすことができます。この要件は、体積V内の所与の音場を再現するが体積V外では消失する音源Q*という図3に定義されているような追加の要件を可能にします。
空気伝播する音場に対しては、閉表面S上に連続的に分布するモノポールとダイポールによって音場は与えられ、外部体積へのフィードバック効果なしに、すなわち体積Vの外側の音場を変化させることなしに、体積Vの内側のオリジナルの音場を完全に補正します。(図4参照)
これは入射波音場を受けるだけで変化はさせない2次音源-Q*を有するアクティブな吸収体により実現されます。また、一次音場から二次音源に伝送されるパワーは、二次音源によって抽出され、必要に応じて、他の場所で再生されます。ここでは、体積V内で吸収された元のパワーが、代替音源である-Q*によって引き継がれます。
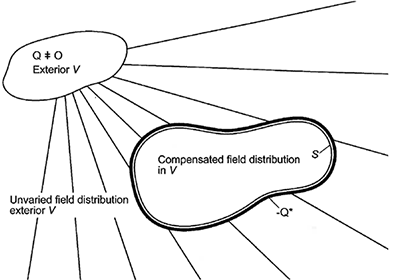
図4 体積Vの外側の体積へのフィードバックなしでのVの音場補正
図4の様に、外部音場を変化させないため表面Sに到達するパワーを吸収するだけではなく一部では放射する配置以外では、表面Sでパワーを吸収する音源-Q*による音源分布があります。このようなアクティブな吸収体によって生じる音場の例を図5に示します。
ここで、エネルギー関係を考えると少し複雑で、それぞれの場合に応じて決まります。2次音源によって生成される音場は、一次音源に立ち返って作用し、エネルギー放射を変化させます。こういったエネルギー相互作用のいくつかの単純かつ例示的な例はいくつもあります。
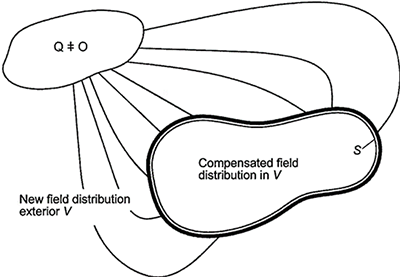
図5 体積V内の純粋な吸収音場の補正
体積V内の音場の再現は、体積V外の音場に追加の制約なく、よりシンプルな音源配置でも達成できます。この補正はもはやフィードバックがなく、体積V外の音場や配置が変化します、すなわち入射波を後方に散乱するようなアクティブな反射機構が組み込まれます。(図6参照)
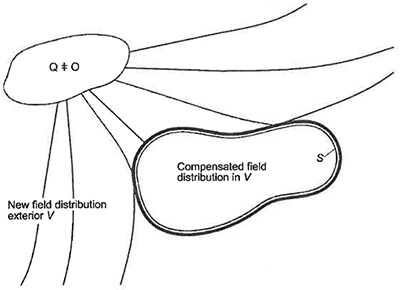
図6 体積V内の反射音場補正
これらの考察は、境界面S上の二次音源分布が入力を抽出することによって一次音場を吸収するか、または入力を再分布することによって一次音場を反射することができるように構成され得ることを示します。
たとえこの反射が、境界Sにおいて力学的エネルギーを抽出も吸収もしないという意味で完全であったとしても、全体的な配置はエネルギー関係を変化させる可能性があります。
反射が一次音源の位置する体積Vの外側に戻るように作用することにより、これらの音源における放射インピーダンスが変化します。結果として、一般にこれらの音源のパワーの放射を変化させます。
実際の状況におけるパワーとエネルギーの関係の解析では、この効果は二次音源による直接的なパワーの抽出よりも重要である傾向があります。
ホイヘンスの原理に基づく形式論は他の媒体にも適用することができます。理論的にはこのような類似性は、自己随伴微分演算子によって定義される任意の境界値問題に対して見られるキルヒホッフの法則の公式に等しい積分関係から始まります。一般的な、せん断変形を有する弾性固体の場合について、このような関係が見出されます。また音響放射に関して重要である、薄板の曲げ波の場合にも類似の式が導かれています。
このような考察は、アクティブシステムの理論的解析には本質的に貢献しましたが、実際の実現のための出発点としては殆ど役に立ちませんでした。これは、主に、二次音源の離散化および空間的拡張の影響を予測するのが困難であることに起因します。
それにもかかわらず、ラウドスピーカーで音場の多次元伝播を遮蔽する際の基本的な実験は、これまでの理論的アプローチを理想化したものに基づいており次回以降でその具体例を紹介します。