オートモーティブ・ソリューション部
03-3245-1058
伝達関数を求める方法はいくつかありますが、一般的な手法として「ハンマリングによる伝達関数測定」と「加振器による伝達関数測定」があります。 ハンマリングによる伝達関数測定は、その手軽さによって、昔から広く実施されてきております。 今回は「ハンマリングによる伝達関数測定」に関して、初学者でもわかりやすく解説します。
ハンマリングとは
伝達関数測定の必要性
伝達関数とは、入力と出力の関係を表す数学的な関数で、入力信号と出力信号の比として表現されます。
機械構造物が発生する振動・騒音の大きな原因のひとつが共振現象です。
共振周波数は各構造物固有のものです。
設計図面の段階で有限要素法などを使って、これらの固有値、モードを計算で求めます。
複雑な構造物の場合、計算値とは違った結果になる事が多いため、出来上がった実際の構造物に強制加振を行い伝達関数を測定します。
測定された伝達関数から共振周波数(固有振動数)と振動モードなどがわかります。
1.原理
構造物にインパクトハンマーや加振器を使って強制加振力を与え、 発生した振動を主に加速度計を使って測定し、伝達関数を計算します。 式で表すと以下のようになります。

2.最小構成
ハンマリング試験で使用する計測器は、FFTアナライザ、加振用インパクトハンマー、加速度計から構成されます。それぞれの役割は次のようになります。
①インパクトハンマー:加振力の計測、加振タイミングの取得
②加速度計:加振に対する応答(加速度)の取得
③FFTアナライザ:データ収録、FFT演算

3.何故ハンマリングなのか
メリット- セッティングが簡単で、加振器を設置する手間が省ける
- 一回の加振で幅広い周波数範囲のエネルギーが得られる
- ローディングマスが小さい ・ローコスト
ハンマリング 間違いあるある
ハンマリングに関する間違いが多い事例をまとめてみました。
衝撃試験およびモーダル解析において、コヒーレンス関数(coherence function)は、入力(励振)と出力(応答)との間の信頼性を定量的に評価する指標として広く用いられている。本項では、コヒーレンス関数の定義とその正しい解釈、および平均化の重要性について解説する。
1. コヒーレンス関数の定義
コヒーレンス関数 γ²(f) は、ある周波数 f における入力信号 x(t) と出力信号 y(t) の関係性の強さを示すものであり、以下の式で定義される:
2. 平均化が必要な理由
コヒーレンスは平均化された測定結果に対して定義される関数であり、単一回の測定(平均回数 N = 1)に対しては、正確な評価が不可能である。平均が1回であれば、変動が存在しないため、任意の信号でもγ²(f) =1となる。
3. 結論
コヒーレンス関数は、入力と出力の相関関係を評価する上で非常に有用な指標であるが、その正確な評価には複数回の測定と平均処理が不可欠である。平均が1回のみである場合、コヒーレンスが1であっても、それは測定の妥当性を担保するものではない。したがって、衝撃試験においてコヒーレンスを信頼性の指標とする際には、測定の平均回数とデータの変動性に十分注意を払う必要がある。
モード解析を実施する際には、構造の節点に基準加速度計や応答点を配置してはならない。ノードとは、特定のモードにおいて構造の変位または応答が理論上ゼロとなる位置であり、ここにセンサを設置した場合、正確な周波数応答関数(FRF)を得ることができない。
1. FRFと節点の関係
FRF(Frequency Response Function)は、加振力に対する構造の応答(変位、速度、加速度など)を周波数領域で表した関数である。基本的に、FRFは入力と出力の間に有意な伝達関係が存在する場合にのみ意味を持つ。構造のあるモードにおける節点では、出力信号はゼロとなるため、FRFもまた無意味または非常に低い値となる。2. 実例1:片持ち梁構造における誤った配置
あるグループが大型の片持ち梁構造のモード試験を実施した際、低周波加速度計を構造ベース部に設置した。これは、センサが落下するリスクを回避する目的であったが、結果としてセンサの設置位置が節点に近い領域となり、測定された応答はほとんどゼロに近いものとなった。このため、得られたFRFは非常に貧弱なものとなり、試験の有効性が著しく損なわれた。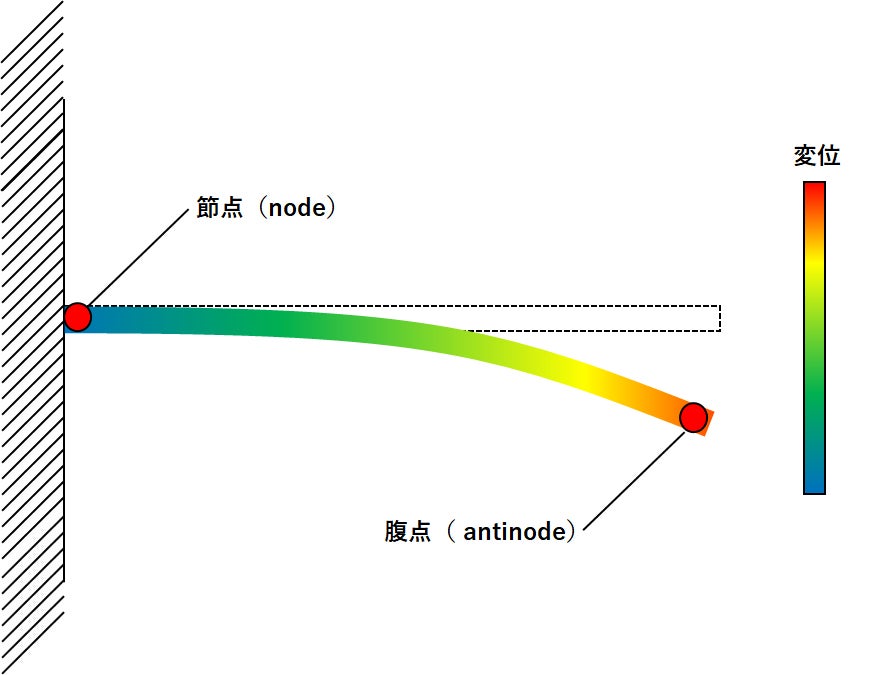
3. 実例2:リブパネル構造での測定位置の偏り
別のケースでは、リブ構造を有するパネルキャビネットの試験において、剛性の高いリブの交点ばかりに加速度計を設置していた。この構造における主なモードは、パネル部のたわみによって形成されるものであったが、測定対象にはパネル面が含まれていなかった。その結果、すべてのセンサは実質的に各モードのノード上に配置されたことになり、ほとんど意味のないデータが数か月にわたって取得されてしまった。4. 測定位置の選定における注意点
モード解析では、応答が期待できる位置(振動の腹点)にセンサを配置する必要がある。これは以下のような原則に従うことで達成される:- ノード位置(構造の変位がゼロとなる点)は避ける
- 応答が最大となる**腹点(アンチノード)**に近い位置を選定する
- 試験前に有限要素解析(FEA)や予備試験を用いて、モード形状を推定しておくことが望ましい

5. 結論
モードの節点に基準点や応答点を配置することは、FRFの取得において致命的なエラーとなる可能性がある。これは、構造がモード的に無応答な位置にセンサを設置することにより、測定結果に意味を持たせることができなくなるためである。適切なモード調査を行うには、対象構造の変形特性を事前に把握し、応答が十分に得られる測定点を選定することが必須である。これにより、信頼性の高いモーダルデータの取得が可能となり、構造解析や製品開発における精度が大きく向上する。
構造物の動特性を測定する際、加速度計やセンサなどの計測機器の質量が測定対象に与える影響は無視できない。この**質量負荷効果(Mass Loading Effect)**は、特に軽量な構造や高周波帯域の測定において顕著であり、得られる周波数応答関数(FRF)に誤差を生じさせ、固有周波数や減衰特性の評価に影響を及ぼす可能性がある。
1. 質量負荷効果の基本的な原理
計測機器が構造体に取り付けられると、システムの局所的な質量分布が変化する。この追加された質量により、局所的な剛性と慣性のバランスが変化し、以下のような現象が生じることがある:- 固有周波数の低下
- モード形状の局所的な変化
- FRFの振幅または位相の歪み
2. 質量負荷の影響が顕著であった実例
1980年代初頭に実施されたある試験では、潜水艦推進システム用の絶縁コンポーネントのインピーダンステストが実施された。テストは、当時としては先進的であった「デジタルステップサイン法」により、5 kHzまでの周波数範囲で実施されており、1回の測定に約3時間を要した。高い信頼性を求められる試験であったため、年間を通じて24時間体制の測定が行われ、数多くの構成について詳細な記録が残された。この試験における測定構成には、エアバッグ上に設置された2トンのコンクリートブロックが含まれていた。試験の正確性を確保するために、全てのセンサと構造物の取り付け条件は厳密に管理されていた。
しかし、試験終了から3か月後、データ評価を担当していたアナリストから、いくつかの測定において約180 kgの質量変化が存在している可能性があるとの指摘があった。調査の結果、一部の夜間測定において、担当していた学生が測定中にコンクリートブロック上で就寝していたという事実が判明した。これは、試験中に構造物上に人間の体重が加わったことで、想定外の質量負荷が生じていたことを意味する。
3. ログブック管理の重要性
この問題が特定された背景には、試験ごとに詳細な**ログ(試験記録)**が適切に保管されていたという点がある。ログには、試験条件、担当者、使用機材、実施時刻などの情報が記録されており、問題のあった測定を迅速に特定することが可能であった。結果として、質量負荷の影響を受けたと考えられる一部の測定は評価対象から除外され、追加の測定が実施された。この事例は、ログ管理の重要性と、見過ごされがちな質量負荷効果が測定精度に与える深刻な影響を強く示している。
4. 結論:質量負荷への配慮と記録管理
質量負荷効果は、構造物のモーダル試験やインピーダンス測定において測定誤差の一因となり得る重要な要素である。その影響は時に顕著であり、場合によっては測定結果の信頼性を完全に損なう可能性もある。したがって、以下の点に注意を払うことが望まれる:
- センサの質量と取り付け位置の影響評価
- 軽量または高周波構造に対する適切なセンサ選定
- 試験時の不要な物理的干渉(例:作業者の接触)を防ぐ管理体制の整備
- 詳細なログブックの保管と活用
ハンマリング試験(衝撃応答試験)を実施する際、**ダブルハンマリング(二重打撃)**が発生することはしばしば避けられない。理想的には、1回の明確な衝撃によって構造物の応答を評価することが望ましいが、実際の試験現場では、ハンマーチップの跳ね返りや不適切な打撃動作などにより、短時間のうちに複数のインパクトが生じることがある。

1. ダブルハンマリングの認識とその影響
ダブルハンマリングが発生した場合、構造体はそれに応じた実際の力履歴に基づいて応答する。つまり、たとえ試験者が1回の打撃を意図していたとしても、構造物が受けた物理的な入力が2回の衝撃であれば、その構造応答(加速度、速度、変位)は実際に複数のインパクトに基づいて変化する。このため、測定された**周波数応答関数(FRF)**やインパルス応答関数には、二重インパクトによる複雑な力履歴が反映され、評価結果の正確性に影響を与える可能性がある。
2. フォースウィンドウ処理による誤った修正手法
一部の試験エンジニアは、ダブルハンマリングの影響を回避するために、**フォースウィンドウ(力信号に対する時間窓処理)**を使用して、2回目の衝撃部分を強制的にゼロ化しようとすることがある。これは、「不要な二度目の衝撃を意図していないのだから、データ処理で除去すればよい」という考えに基づいている。 しかしながら、これは測定理論上および物理的現象の観点から誤ったアプローチである。構造物は実際にダブルハンマリングによる励振を受けており、すでにその入力に基づいた応答が生じている。後処理で入力信号の一部をゼロにしても、出力信号にはダブルハンマリングに起因する応答が残存しているため、整合性のあるFRFやインパルス応答関数を得ることはできない。3. 正しい対処法
ダブルハンマリングの影響を回避するには、以下のような試験設計段階での対策が求められる:- 適切なハンマーチップ(材質や硬さ)の選定
- ハンマーヘッドの反発特性の調整
- 熟練した打撃手法の習得と実施
- 試験後の信号確認と、必要に応じた再測定の実施
4. 結論
インパクト試験においてダブルハンマリングが発生した場合、その影響をフォースウィンドウ処理によって除去しようとする試みは不適切である。構造はすでにダブルハンマリングに対して応答しており、力信号のみを加工しても、出力信号との整合性は失われる。したがって、信頼性の高い測定データを得るためには、物理的に正確な入力を行うことが最も重要であり、後処理による修正では不十分である。実験精度を確保するには、試験前の準備と技術者の熟練度、ならびに異常信号の識別と管理体制の整備が不可欠である。
本稿では、平均化処理の本質的な誤用に関する実例を通じて、適切な実施方法を解説する。
1. 事例紹介:異なる打点を用いた平均化の誤り
ある試験では、比較的単純な構造体に対してモーダル解析が行われたが、その結果得られたモード形状は物理的整合性をまったく持たない、不自然な応答パターンとなっていた。初期診断では、センサの取り付けミスやチャンネル設定の誤りが疑われたが、詳細な確認の結果、測定手順そのものに重大な誤解が存在していることが判明した。具体的には、測定対象には25か所のポイントが設定されていたが、試験エンジニアは各ポイントごとに25回の平均処理を行っていた。その際に、25回の衝撃打撃をすべて異なるポイントで実施し、それを1つの平均FRFとして記録していた。すなわち、1つのFRFが、構造の25か所すべての打点の応答を平均化した結果として記録されていた。
この処理を25点すべてに対して繰り返した結果、全体のモード形状は無意味なデータの集合となり、整合性のある振動解析が成立しない状態となった。
2. FRFの平均化における正しい原則
FRF(Frequency Response Function)は、特定の入力点(打点)と出力点(応答点)における線形な力-応答関係を周波数領域で表記するものである。平均化処理の目的は、同一の入力条件下で複数回測定した結果を統計的に安定化させることにある。そのため、平均化は必ず、同一の打点・同一の応答点の組み合わせに対して行わなければならない。異なる打点を組み合わせた平均は、物理的に意味のある関数とはならず、系の特性を適切に反映しない誤ったFRFとなる。
3. 誤った平均化がもたらす影響
誤った平均処理によって得られたFRFは、以下のような問題を引き起こす:- モード形状の非物理的な歪み
- コヒーレンス関数の極端な低下
- 再現性のない共振ピーク
- モードパラメータ(固有周波数、減衰比、モードベクトル)の誤認識
4. 結論と推奨事項
モーダル試験においてFRFの平均化を行う際は、常に同じ入力点(打点)で複数回の測定を行い、それを平均処理するという基本原則を厳守する必要がある。これを怠ると、得られるモード情報は信頼性を欠き、試験全体が無意味なものとなる可能性がある。測定の整合性は、正しい手順と基本原則の理解によって保証される。特に多点測定を伴うモーダル試験では、平均化手法とデータ収集の対応関係を明確にし、誤った手順を排除するための教育とレビュー体制を整備することが重要である。
1. 座標系の明示は基本中の基本
位置および方向情報の定義は、本質的には非常に単純な作業である。座標系(x, y, z軸)を試験体または設置環境に対して一貫して定義し、その情報をセンサの設置方向およびモーダル解析ソフトウェアに正確に反映させることが求められる。この作業を確実に行うための有効な手法の一つとして、試験準備段階で座標系を物理的に明示しておくことが挙げられる。例えば、床面にテープを貼り、x軸、y軸、z軸の方向を明示的にラベリングすることで、全ての関係者に共通の座標基準を提供することができる。
2. 誤った方向指定がもたらす影響の事例
あるエンジンブロックのモーダル試験において、予想される剛体モード(低周波数)の代わりに、約10 Hzの変形モードが検出されたという報告があった。このような高い周波数帯におけるモードは、試験構成から見て現実的に考えにくい現象であったため、点および方向情報の指定に誤りがないかが疑われた。当初、試験担当者は「経験豊富なモーダルエンジニアであり、方向情報の指定には自信がある」と主張していたが、測定データを精査した結果、エンジンブロックの一面に取り付けられたX方向加速度計が、指定された方向と180度逆向きに設置されていたことが明らかとなった。
このような誤配置は、加速度の符号反転を引き起こし、全体のモード形状の整合性を損なう。位相補正を適用し、正しい向きに修正した後は、剛体モードが期待どおりの低周波数で現れ、モード解析結果は適切なものとなった。
3. 正しい座標管理のための推奨事項
以下に、モーダル試験における座標系と方向情報を正確に管理するための実践的な対策を示す:- 試験準備段階で座標系を明示(テープや矢印マークによる物理表示)
- 全センサの設置方向を記録・写真撮影
- 幾何情報(ポイントと方向)のドキュメント管理とレビュー
- 方向情報の整合性を確認するための初期試験信号の位相チェック
- モーダルソフトウェア内の方向設定と現物の一致確認
4. 結論
座標系および方向情報の管理は、モーダル試験における最も基本的でありながら重要な手順である。手順自体は単純であるが、わずかなミスが測定結果全体の信頼性を損なう可能性がある。物理的な方向表示、設置記録の明確化、データレビュー体制の構築など、シンプルな確認作業を怠らないことが、信頼性の高いモード解析の鍵となる。
本稿では、有限要素モデルに過度な信頼を置いたことで生じた試験設計上の問題を取り上げ、モデル活用時の留意点を整理する。
1. 有名な格言とその背景
構造試験の世界には、以下のような有名な皮肉がある:「テストエンジニア以外は皆テストを信じ、アナリスト以外は誰もモデルを信じない。」
(“Everyone believes the test except the test engineer, and no one believes the model except the analyst.”)
この言葉が示すように、理論解析と実測データの間にはしばしば乖離が存在する。特に、有限要素モデルが十分に検証・更新されていない場合、その信頼性は大きく損なわれることがある。
2. 実例:人工衛星構造のモーダル試験における誤判断
1990年代、ある大型の人工衛星構造物に対してモーダル試験が実施された。この構造は、巨大な地震質量(seismic mass)に取り付けられた長大な片持ち梁構造であり、複数の加振機が必要とされる複雑なシステムであった。事前に実施された有限要素解析では、構造の長さ方向に沿って複数のシェーカー位置が選定されたが、水平方向のうち1軸にのみ加振装置が配置され、もう1軸には加振機が設置されなかった。その理由として、解析担当者は「すべてのモードが既存の加振方向で十分に励起される」と主張した。
しかし実際には、モデルには複数の不正確な集中質量要素(lumped mass elements)が含まれており、位置や値が誤っていた。その結果、事前解析の内容は偏ったものとなり、モーダル試験に必要な励振方向の一部が欠如する事態が発生した。
3. 有限要素モデルを使用する際の留意点
有限要素モデルは、モーダル試験の設計を支援する上で極めて有用なツールであるが、以下のような前提条件と限界を正しく理解しておく必要がある:- モデルは理論仮定に基づく近似解であり、実構造とは乖離が存在しうる
- 要素の定義ミスやパラメータ誤入力が解析結果を大きく歪める
- 境界条件や拘束条件の理想化に注意が必要
- FEMの結果は、実測によって検証されて初めて信頼できるものとなる
4. 参考点(Reference Point)の選定は慎重に
モーダル試験における励振点および応答点の選定は、試験成功の鍵となる。有限要素モデルがある場合は、モード形状を参考に励振方向や測定点の候補を設定することができるが、モデルの正確性が不明な段階では、それに依存しすぎない柔軟な設計判断が求められる。特に以下のような配慮が推奨される:
- 異なる励振方向を含めた複数方向での励振検討
- モード励起のdriving point FRF や MAC(Modal Assurance Criterion)解析の実施
- 試験後の**モデル更新(Model Updating)**を前提とした検証的アプローチの採用
5. 結論
有限要素モデルは、モーダル試験の設計支援において非常に有効なツールである一方で、その信頼性には限界があり、未検証のモデルに基づく一方的な設計判断は危険を伴う。FEMはあくまで仮定に基づく解析結果であり、実測データとの整合性を通じてその有効性が確認されるべきである。試験設計においては、モデルと実測の両方の視点をバランスよく活用する柔軟な姿勢が不可欠である。
モーダル試験の成功において最も重要な要素の一つは、試験の各ステップを論理的に考え抜く姿勢である。手順や装置の進化によって自動化が進んだ現代においても、測定結果の信頼性と意味を確保するためには、常に「なぜその方法を用いるのか」を意識することが不可欠である。
1. FRFの信頼性は“理解”によって支えられる
周波数応答関数(FRF)は、構造の入力と出力の物理的関係を数値的に表すものであり、モード解析の基盤をなす情報である。このFRFを正確に取得するためには、励振方法、センサの設置、データ取得条件、平均化手法、方向情報など、あらゆる測定要素を明確に理解し、意図的に選定する必要がある。2. 手順の“惰性”による測定の危険性
試験現場においてよく見られる誤った姿勢として、「昔からこうやっているから正しいはずだ」という思考停止が挙げられる。形式的な手順の継承は、理論的な裏付けがなければ意味を持たない。このような態度で取得されたデータは、表面的には整っていても、物理的整合性を欠いたまま運用されてしまうリスクが高い。3. 問うべき最初のステップは「なぜ」
信頼性のあるモーダル試験を行うために、最初に実施すべきは「なぜこの手順を取るのか」「なぜこの方向に加振するのか」「なぜこのセンサを選定したのか」といった基本的な前提条件への問いかけである。これにより、作業手順が単なるルーチンではなく、物理的・理論的裏付けのある選択となる。4. モーダル試験は“考える技術”である
モーダル試験は、ワンタッチで完了する自動化技術ではない。選択肢を選ぶだけで結果が保証されるような「ボタンを押すだけの技術」ではなく、測定者の理解と判断が結果の精度を左右する試験手法である。たとえ測定機器やソフトウェアが進化したとしても、その運用における判断と最終的な解析は技術者の思考に依存する。技術者自身が“考えることをやめない”限り、モーダル試験は今後も進化し続けるだろう。
5. 結論
モーダル試験における「正しいFRFの取得」とは、単に手順通りに測定を行うことではない。その測定が物理的に意味のあるものか、選択された手法が妥当であるかを常に意識することが求められる。思考は選択肢ではない。必須である。
自動化技術が進んだとしても、モーダル試験は依然として**“考える人間”によって支えられている**。技術的正確性と論理的整合性を保つためには、全ての測定工程において「なぜ」を問い、理解した上で判断を下すことが重要である。
測定動画
ハンマリング試験効率化機能
ハンマリングでは共振点以外にもFRF、位相、コヒーレンス等多くの物理量を監視する必要があります。
OROSではダブルハンマリング検知、コヒーレンス監視に加え、条件を満たさないデータを自動的にリジェクトする機能があります。
OROS 動画コンテンツはこちら
FAQ
A: 共振周波数の部分では、位相は90°遅れます。位相の情報から、測定対象の共振周波数がどこにあるのかを正しく把握することができます。
また、共振周波数の部分で位相が90°ずれるということは、実部がゼロとなり、虚部が大きくなります。このことから、実部/虚部表示にすれば、共振周波数がどこにあるのかわかりやすくなります。
A: コヒーレンスも伝達関数同様にクロススペクトラムから求めますが、定義式の元々の形は、「誤差を除いた応答と誤差が混入したままの応答の比」です。
ここで、「誤差を除いた応答」というのは、「入力のFFT分析結果(スペクトラム)に、測定された伝達関数を掛け合わせることで予想された応答」を示し、「誤差が混入したままの応答」は応答のスペクトラムを示します。つまり、「応答にどれだけの誤差が含まれているか」ということを表す量でしかありません。
A: ハンマリング試験において使用されるウィンドウ関数は2種類あります。
① フォースウィンドウ
入力(ハンマー)信号側にかけるウィンドウ関数で、ハンマーのインパルス波形以外の部分を強制的にゼロにします。ノイズの除去ができるので、コヒーレンスの向上に役立ちます。
② レスボンスウィンドウ
応答(加速度センサ)信号側にかけるウィンドウ関数です。減衰が長く、1FFTブロック長内で振動が収まらない場合、レクタンギュラウィンドウでは、リーケージの影響を受けてしまいます。そのため、端に行くにしたがって、次第に信号を減衰させるようなウィンドウ関数を適用します。ただし、応答波形を無理やり減衰させるため、本来の減衰率と異なってしまいますので、レスボンスウィンドウの形状には注意が必要です。
ハンマリングによる伝達関数の測定の場合、ウィンドウ関数をかけることなく、コヒーレンスの高い伝達関数を得ることができるのが理想的です。しかし、難しい場合が多くありますので、特性を理解した上で、適切なウィンドウ関数を利用することをお勧めいたします。
A: ハンマーの選定には大きさ(重さ)が重要です。主に加振対象の大きさと重さによって使い分けます。大きい・重いものには大きなハンマーを使用し、小さい・軽いものには小さなハンマーを使用します。
大きなハンマーは加振力が大きいため、加振点と応答点の位置が離れている場合でも、S/N比よく計測ができます。しかし、小さいものを加振するのには向きません。一方で、小さなハンマーは叩きやすく、高い周波数まで加振できます。しかし、加振力が小さいので加振点と応答点が離れていると、S/N比が低下してしまう場合があります。マスを追加することで、この問題はある程度解決できますが、マスを追加した場合、ハンマーについているセンサの感度が変化しますのでご注意ください。
A: 主にソフト、ミディアム、ハードの3種類があり、加振できる周波数の範囲が異なります。高い周波数までの伝達関数を求めたい場合は、ハードチップにし、高い周波数まで加振する必要があります。もし、高い周波数まで伝達関数を求めるにも関わらず、ソフトチップを使用した場合、伝達関数の高周波側にノイズ(伝達関数がギザギザする)が発生してしまいます。ソフトチップの利点は、低周波側に加振力が集中しているため、S/N比の向上が見込める点にあります。
A: どの程度変化をするのか、表したものが下の図です。測定対象物に対して7% の重さのセンサを付けた場合、約10Hzも伝達関数のピークがずれています。そのため、ハンマリング試験をする際は対象物に対して十分に軽い加速度センサをご使用ください。
加振対象物: 1.39kg
軽量センサ: 0.8g (0.05%)
工業用センサ: 51g (3.6%)
工業用センサ+マグネットベース:101g (7.2%)
機器選定ガイド(基本編)
測定ステップ ① 試験体固定
試験対象物を固定します。一般的な固定法として、対象物の拘束を行わないFree-Free法があります。
柔らかいゴムでつるしたり、スポンジやクッションの上に対象物を設置します。
測定ステップ ② 機材
インパクトハンマー、加速度計(1軸or3軸)、FFTアナライザ(PC)を用意、設定します。
平面的な挙動を知りたい場合は1軸、3次元的な動きを知りたい場合は3軸加速度計を使用します。
※選定方法は「機器選定ガイド」参照
測定ステップ ③ センサー設置
加速度計を試験対象物に貼り付けます。
感度や形状よりも、「重さ」を重視する。小型軽量であるほど良い。
測定ステップ ④ 加振
インパクトハンマーで加振するポイントを決定し、加振する。
この時、ハンマーからの信号を受けFFTアナライザが信号の収録を開始。
測定ステップ ⑤ 分析 収録した結果をFFT分析し、伝達関数を取得する
測定ステップ ⑥ ③~⑤を繰り返す(※モーダル解析を行う場合)
加振位置(ハンマーでインパクトを与える点)を固定し、加速度計を動かしながら③~⑤を繰り返すのが最も簡単。
計測パッケージ例
ハンマリング測定器キット 価格(税込み ¥1,500,000 ~)

アナライザ O4 OROS 製品一覧
FFT分析、3次元カラーマップ分析、時間波形レコード、クロススペクトラム・伝達関数演算
センサ・ケーブル(米国PCB社製) PCBセンサ・オンラインストア
・086C03 PCB社製インパクトハンマー
・012A10 BNCケーブル(3m)
・356A32 三軸ICP加速度計(11.4mm角、感度:10 mV/(m/s2)
・034K10 三軸センサ用BNCケーブル(3m)
オーダートラッキングキット 価格(税込み ¥1,700,000 ~)

アナライザ O4 OROS 製品一覧
FFT分析、3次元カラーマップ分析、時間波形レコード、クロススペクトラム・伝達関数演算
次数比分析オプション NVG-ORD-04
センサ・ケーブル(米国PCB社製) PCBセンサ・オンラインストア
LTレーザータコメータ *電源供給のためにO4の入力1chを使用します。
・070A11 タコメータ電源供給用コネクタ
・012A10 BNCケーブル(3m)
・356A03 三軸ICP加速度計(6mm角、感度:1 mV/(m/s2)
・034G05 三軸センサ用BNCケーブル(1.5m)

