【理化学計測】オウンドメディア:電気化学測定(02)
【理化学計測】オウンドメディア:電気化学測定(02)に関するFAQ
Q複数トレースにまとめてウェイティング設定などを設定したい
FAQ ID:x173
多チャンネル計測を行った場合、Aウエイト、積分などを設定する際に一つ一つトレースを選択してから設定しなければなりません。複数のトレースを選択して一括して出来きますか。
グラフのデフォルト値を設定することができます。
- 以下の手順でユーザ設定のウィンドウを開きます。
V7以降の場合
ホームタブ内の一般ボタンを押します。
V6以前の場合
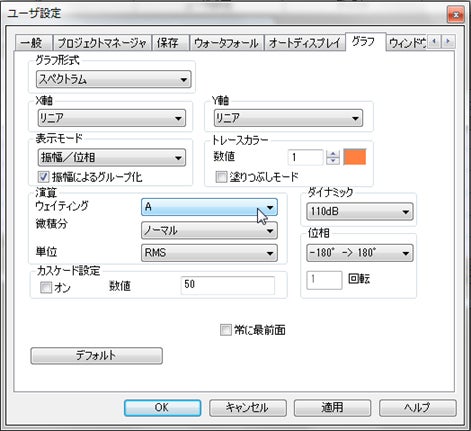
メニュー"ユーザ/ユーザ設定"を選択してください。 - 表示されたダイアログの"グラフ"タブを選択してください。
- "グラフ形式"で希望するグラフ形式を選択して、ウェイティングを設定してください。
次回よりグラフを作成すると指定した形式でグラフが表示されます。
QVersion 7.00 リリースノート
Q疲労寿命推定、S-N線図の作成
疲労寿命推定
頻度解析の結果を利用する典型的な例としては疲労寿命推定があります。
ここでは、S-N線図を用いて材料・製品等の疲労寿命を推定する方法について説明します。
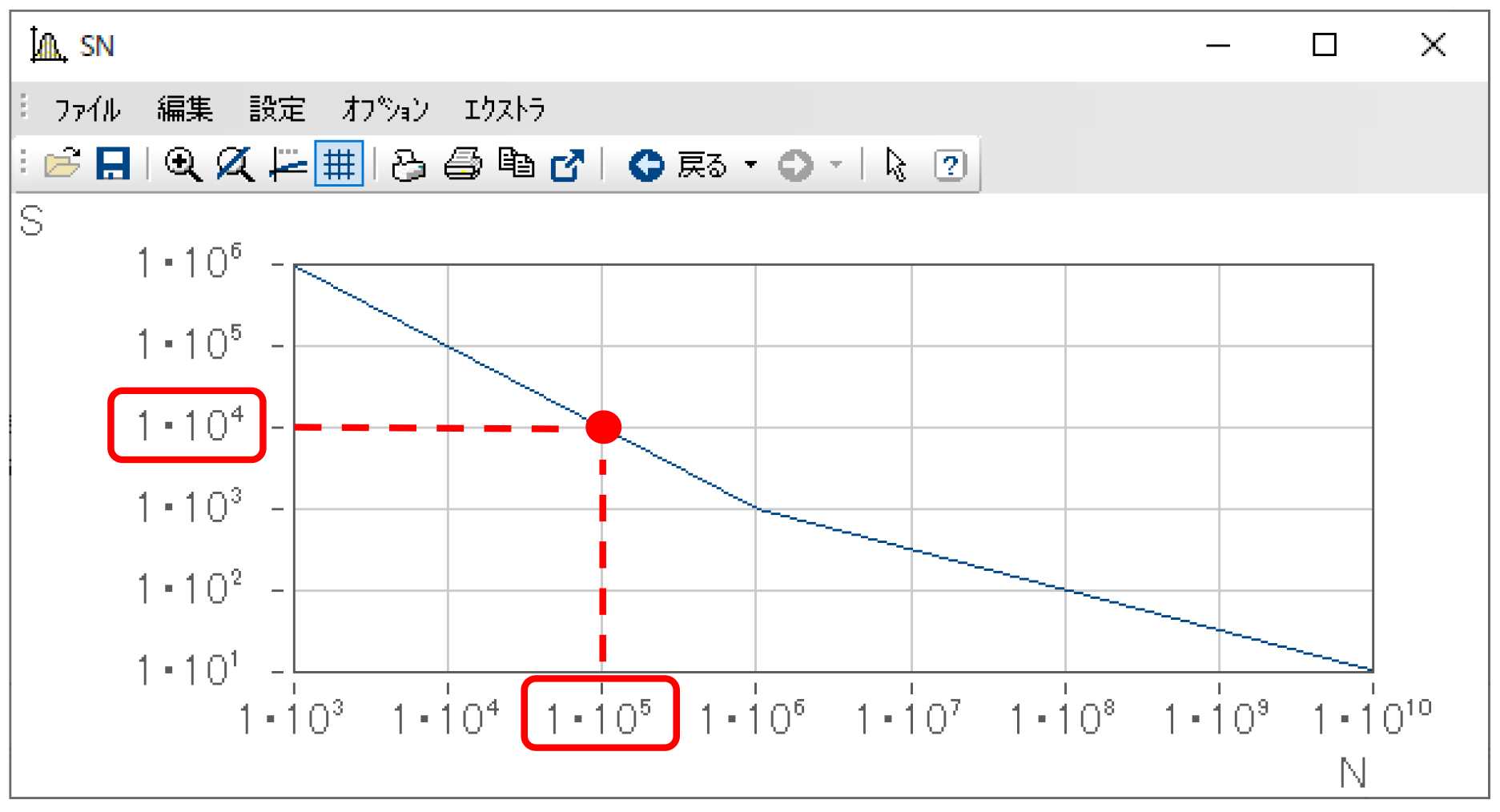
S-N線図とは下図のような曲線で、応力(S)と繰り返し回数(N)の関係を表しており、材料・製品自体の特性を示すものです。
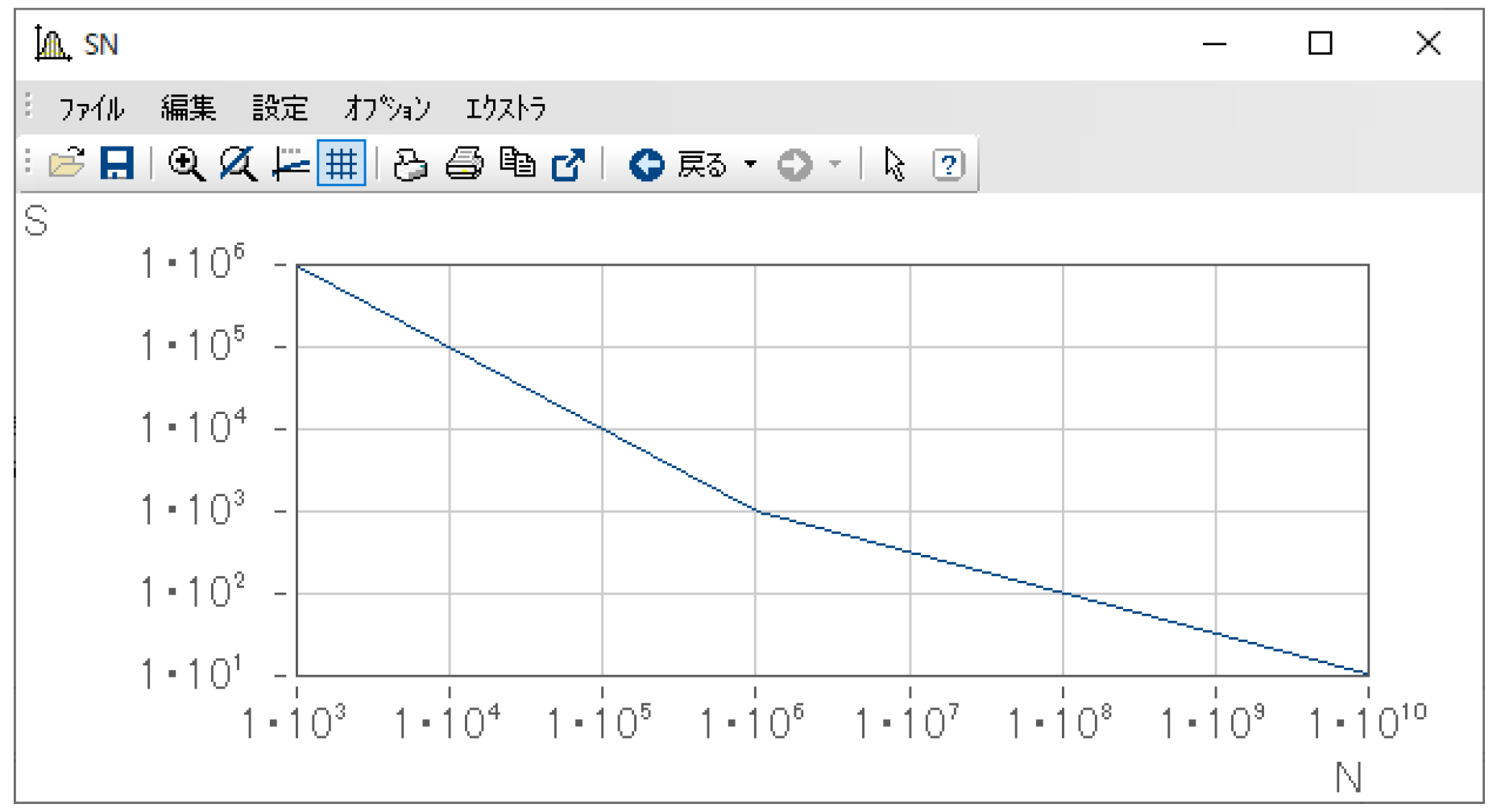
例えば下図に示す1点に着目してみましょう。
これは、このS-N線図が示す対象は、10^4程度の応力(S)を加えられた場合、10^5程度の繰り返し回数で破断・破壊されるということを意味します。
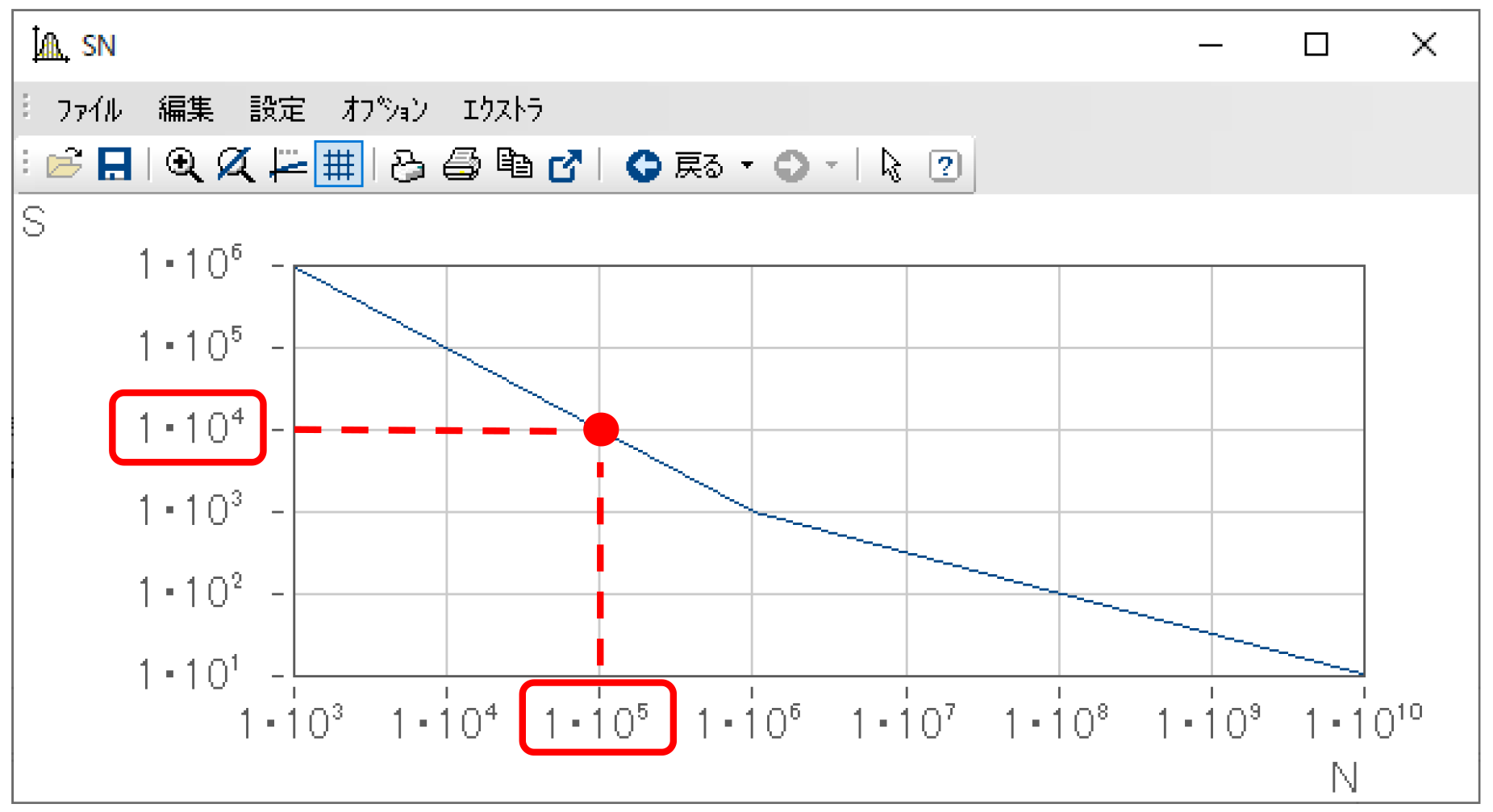
疲労寿命推定では、このS-N線図を元に、まず「ダメージ」を見積もります。
先ほど説明した1点、10^4程度の応力(S)を加えられた場合、10^5程度の繰り返し回数で破断・破壊される、ということは、10^4程度の応力が「1回」加えられた時のダメージは1 / 10^5、と言い換えることができます(=ダメージの累計が1で破断・破壊)。
同じことがすべての応力の値に対して考えられるので、試験データを頻度解析した結果からは、その試験での累計のダメージ、を求めることができます。
そこから、対象の疲労寿命を推定できます。例えば以下のような考え方です。
| 試験データの累計ダメージ | 0.02 |
|---|---|
| 試験データが示す時間(実際の動作環境に換算する) | 10h |
| 推定される疲労寿命 | 10h / 0.02 = 500h |
「試験データが示す時間」は、例えば車両であれば距離[km]で表現してもよいでしょう。その場合は疲労寿命も距離[km]の単位で求められることになります。
次項より、実際にimc FAMOSで疲労寿命推定を行う場合のシーケンス記述について説明していきます。
S-N線図の作成
S-N線図の作成は以下のようにSの配列、Nの配列を作成してそれぞれの値を指定し、それを結合する形で作る方法が簡単です。
作成されたS-N線図のデータはファイルとして保存しておけば、以後の解析に使いまわせます。
; 配列の作成
_S = Ramp(0, 1, 3) ; 最後の3が配列の長さ
_N = Ramp(0, 1, 3)
; S/Nそれぞれの値の設定
_S[1] = 1e6
_S[2] = 1e3
_S[3] = 1e1
_N[1] = 1e3
_N[2] = 1e6
_N[3] = 1e10
; 結合、N(=横軸)が先であることに注意
SN = XYof(_N, _S)
QClsPeak1関数(カウント方法、パラメータについて)
カウント方法について
ClsPeak1関数は、ある参照ラインを設定し、そのラインを超えた2点間の最も大きい極値のみをカウントする、という手法を取ります。
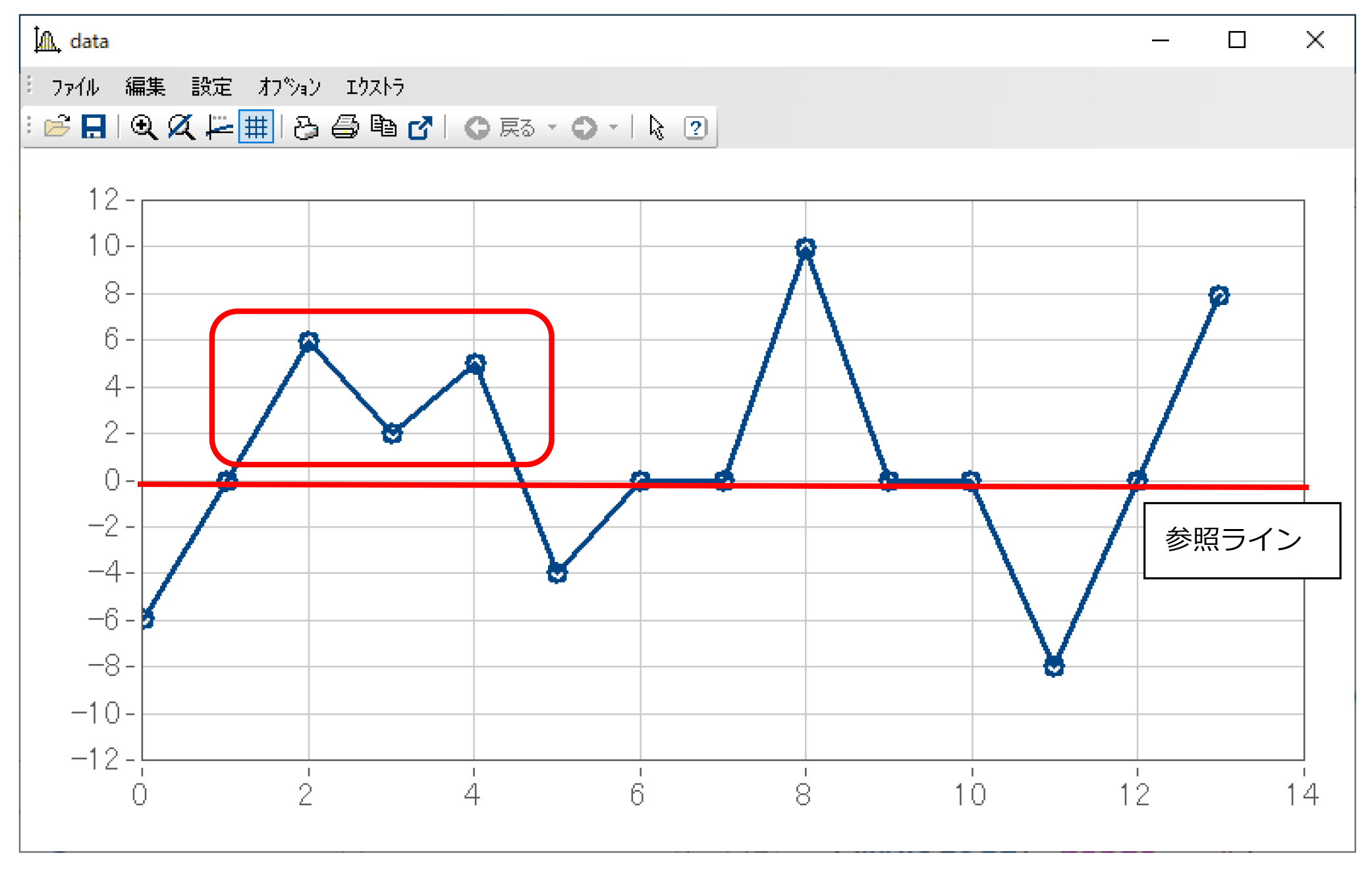
例として下図のデータで、参照ラインとして0の場合を考えます。
そうすると、最初の山はy=6とy=5の2つの極大値の両方が、「参照ラインを超えた2点間」に含まれています。そのため、ここではより大きい極値であるy=6のみがカウントされます。
なお、y=2に極小値も存在していますが、極小値は逆に「参照ラインを下回った2点間」をカウントしていくため、この極小値はカウント対象となりません。
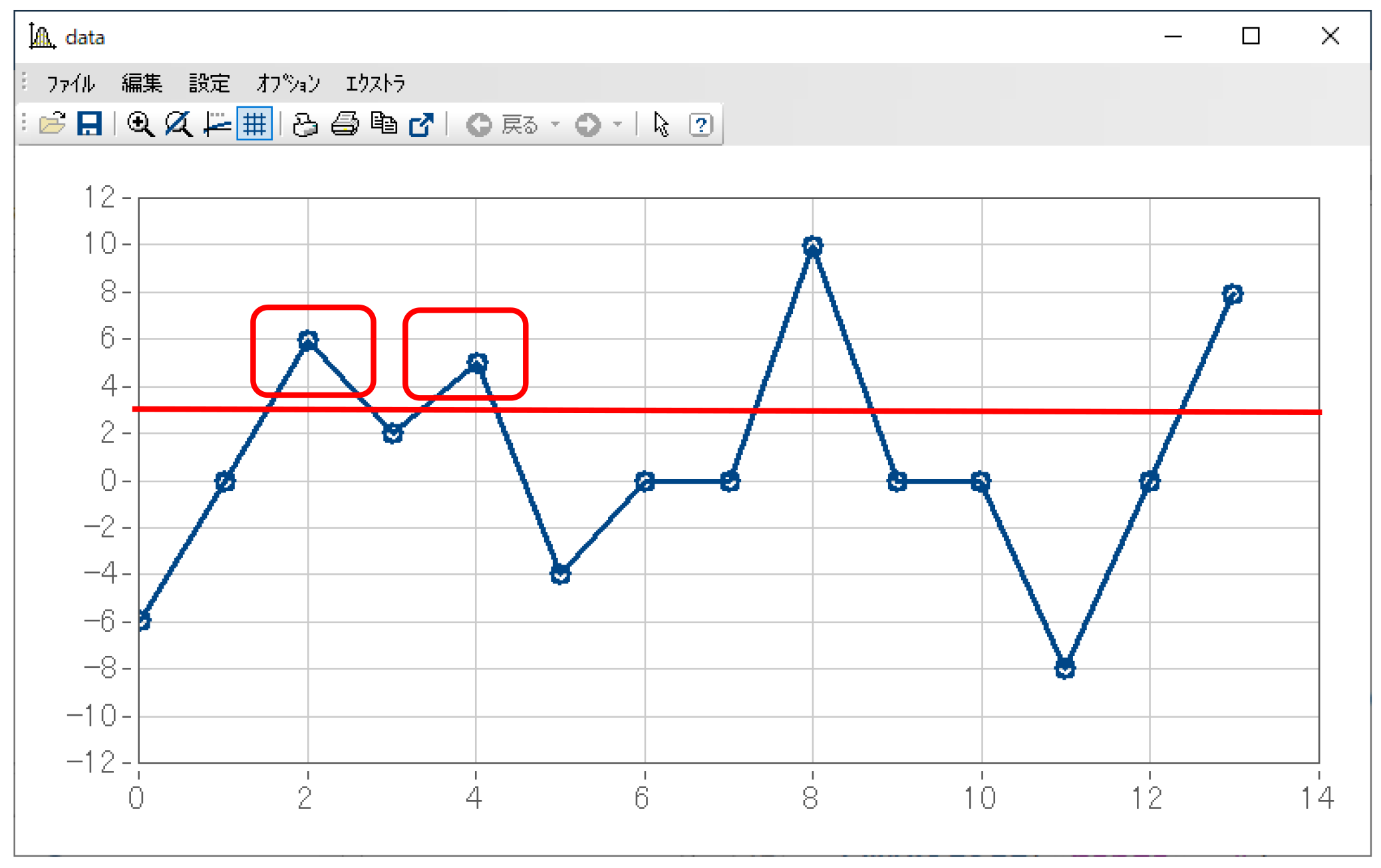
同じデータで、参照ラインとして3の場合としてみましょう。
そうすると、y=6とy=5の2つの極大値は、それぞれ別の「参照ラインを超えた2点間」に含まれています。そのため、この状態ではy=6の極値もy=5の極値も両方カウントされます。
(先ほどの例とは逆に、y=2の極小値はカウント対象となります)
同様の考え方が他の極大値、極小値すべてに対しても行われてカウントされていきます。
なお、データの始点/終点もカウントの対象となります。
関数のパラメータについて
ClsPeak1関数のパラメータは以下のようになります。
Result = ClsPeak1(data, MaxValue, MinValue, Number of bisn, Reference, Hysteresis, Options)
| Result | カウント結果の変数名 |
|---|---|
| data | カウント対象データの変数名 |
| MaxValue | カウントするレンジの上限 |
| MinValue | カウントするレンジの下限 |
| Number of bins | 分類するクラスの数 |
| Reference | 参照レベル |
| Hysteresis | 小さな振動を無視するためのヒステリシスの大きさ |
| Options | カウントする際の挙動に関するオプション設定 |
MaxValue, MinValue, Number of binsは、クラスの設定に関するパラメータです。
例として、下図のように-12から+12までの範囲を6個のクラスにするとします。この時のパラメータは
| MaxValue | 12 |
|---|---|
| MinValue | -12 |
| Number of bins | 6 |
となります。(imc FAMOSのクラスは標準では0から始まります)
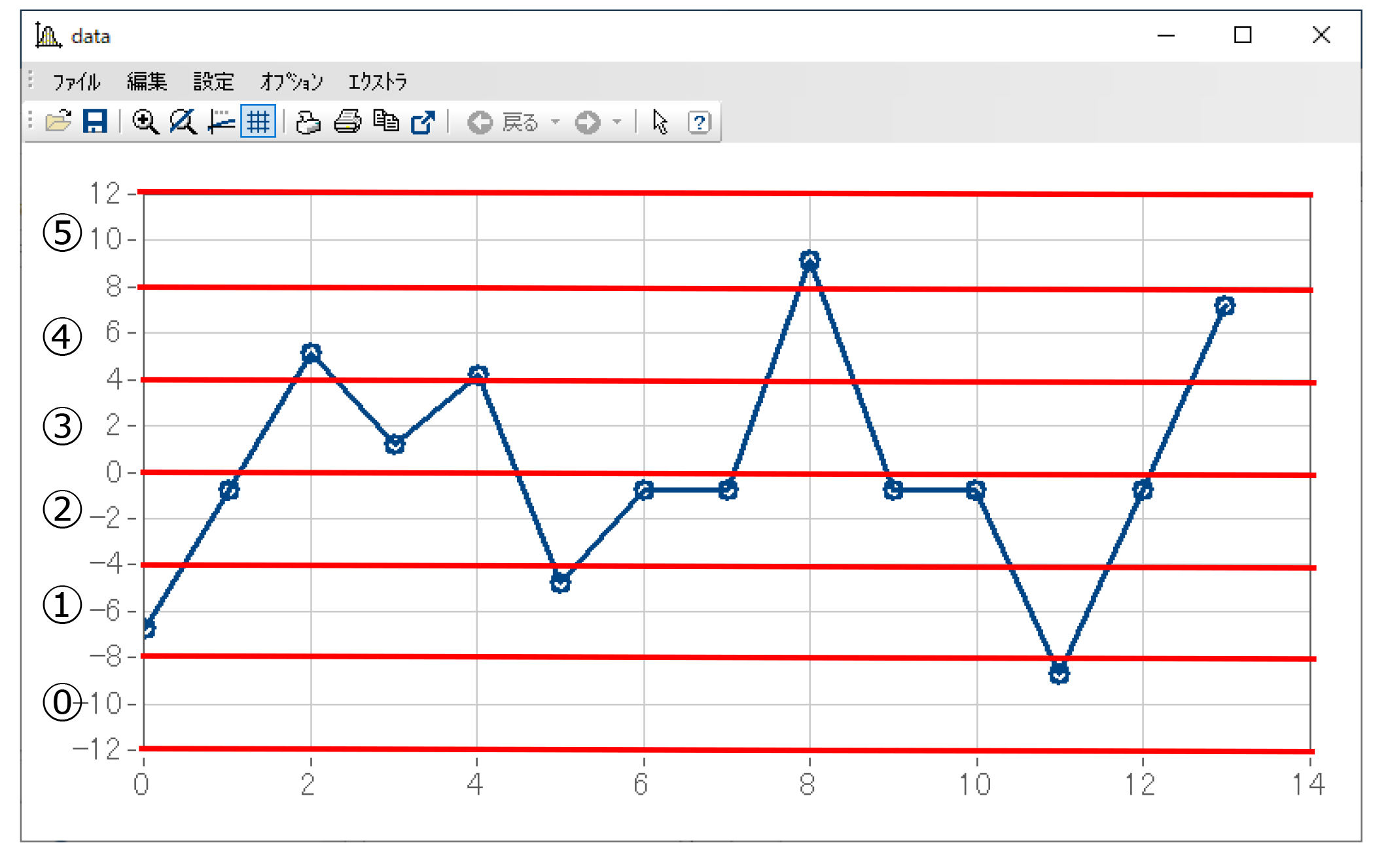
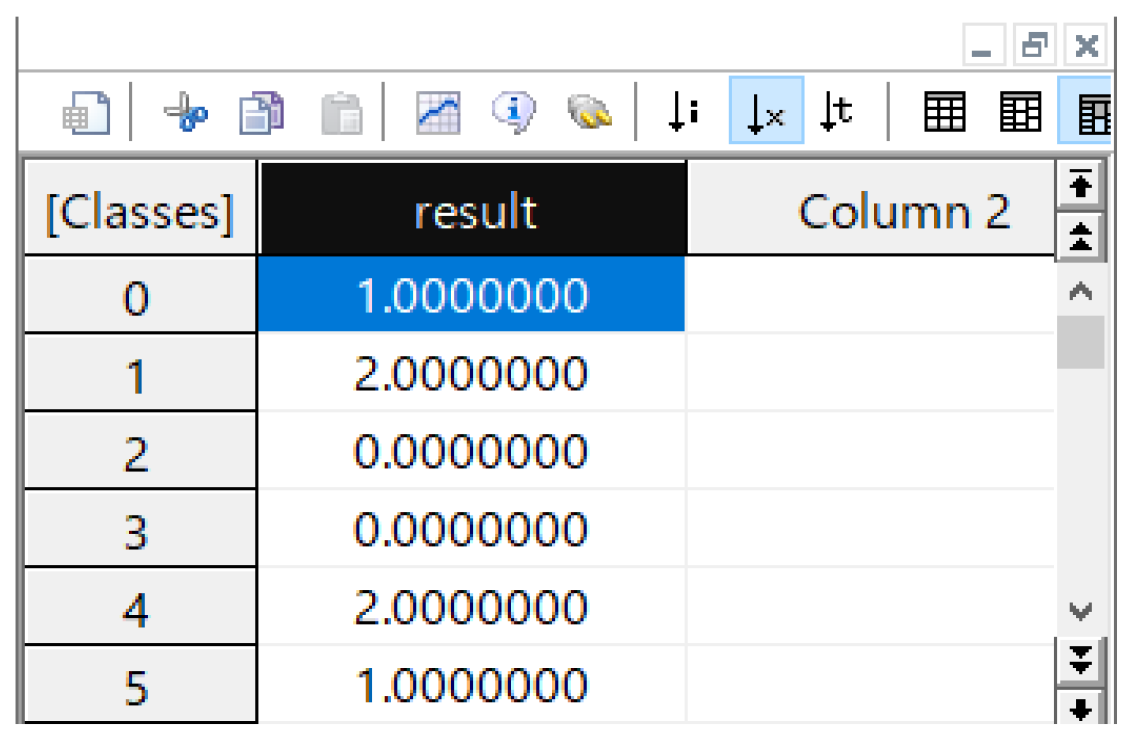
実際の解析例は、下図のようにどのクラスにいくつの極値がカウントされたか、という系列となります。この解析はReference=0で行っています。
クラス3, 4のカウント結果が疑問の方は「カウント方法について」の説明をご参照ください。
なお、このデータは分類のわかりやすさのために、「カウント方法について」のデータとは多少値を変更しています。(クラスの境界に値が乗らないよう)
Reference(参照レベル)の考え方は「カウント方法について」を参照してください。
0を中心に正負に振れるようなデータであれば、0としておくのがよいでしょう。
Hysteresisは微小な振動(ノイズ等)を無視させるためのパラメータです。
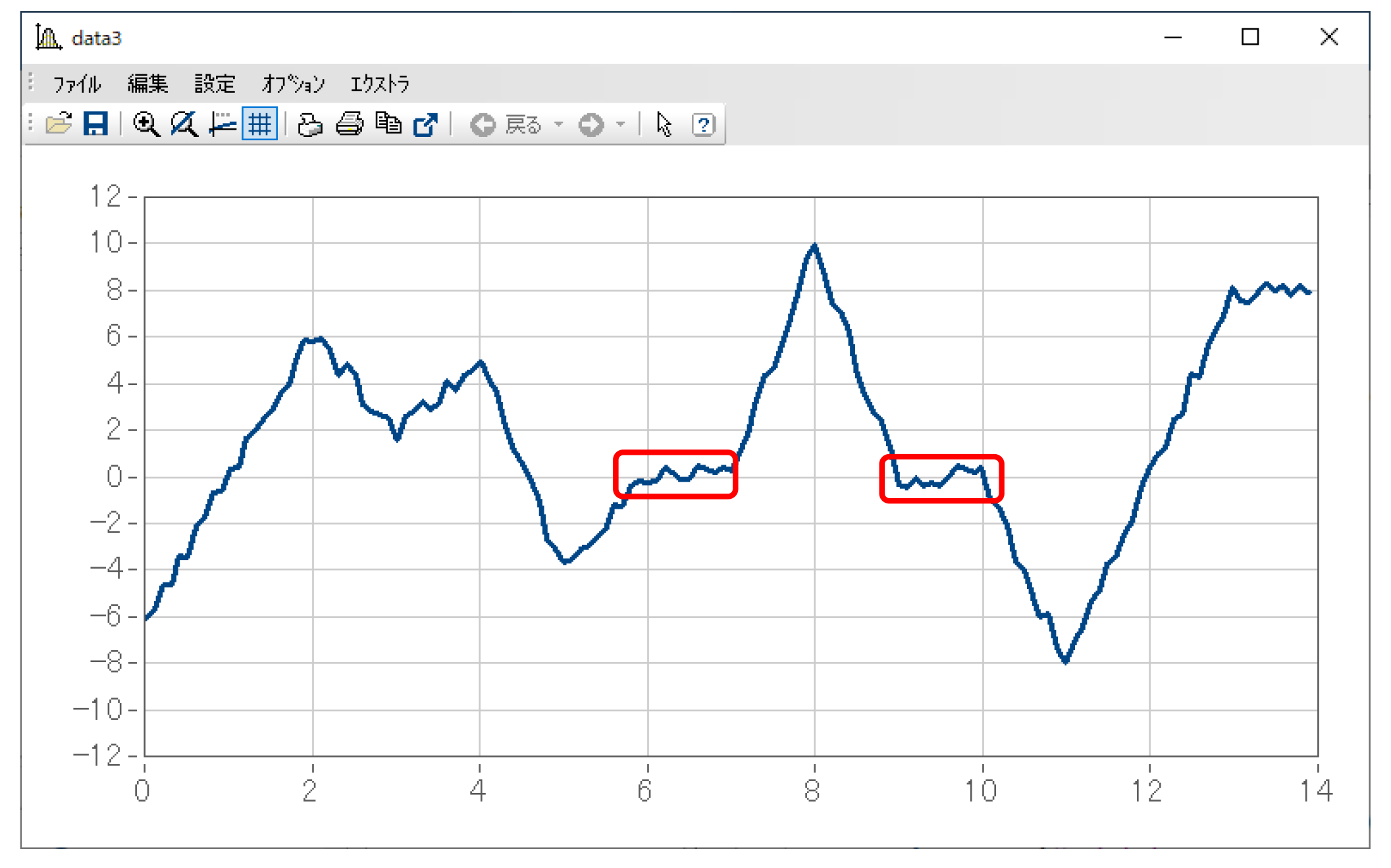
例として、下図のようなデータを参照ライン=0としてそのままカウントした場合、0付近に存在するノイズ成分で余分なカウント結果が出現します。
Hysteresis=1のように設定すると、振幅が1に満たない微小な振動を無視するようになり、実際に欲しい解析結果に近い値が得られるようになります。
optionsはオプション設定用の値で、以下の4つが存在します。
0:オプション設定なし。
1:クラスの上限/下限の外にあるデータもカウントの対象とします。
例えば、クラスの上限が8でy=10の極値がある場合、この極値は上限のクラスに含まれるものとして カウントします。逆にoptions=0の場合はこの極値は無視されます。
2:参照レベルを関数が自動的に決定します。Referenceで設定した値は無視されます。
3:1と2のオプションを同時に適用します。
Qレインフロー法概要
レインフロー法は、振幅の大きさを基準にクラスをカウントしていく手法です。
この振幅の大きさを考える手法は、屋根を流れる雨水の経路をイメージするとわかりやすいです。例として、下図のようなデータがあるものとします。
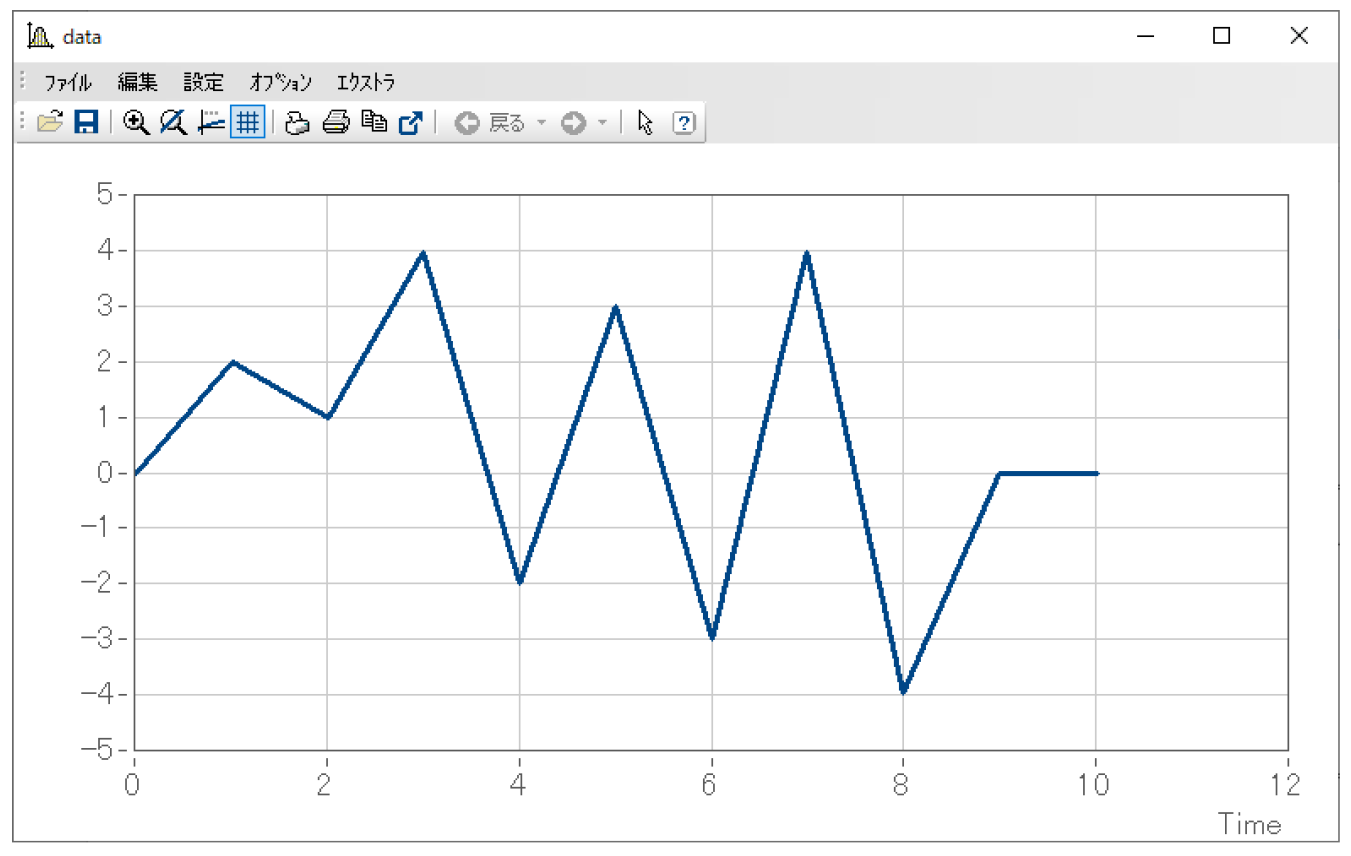
そして、時間軸を下方向にとった下図のような形で考えます。
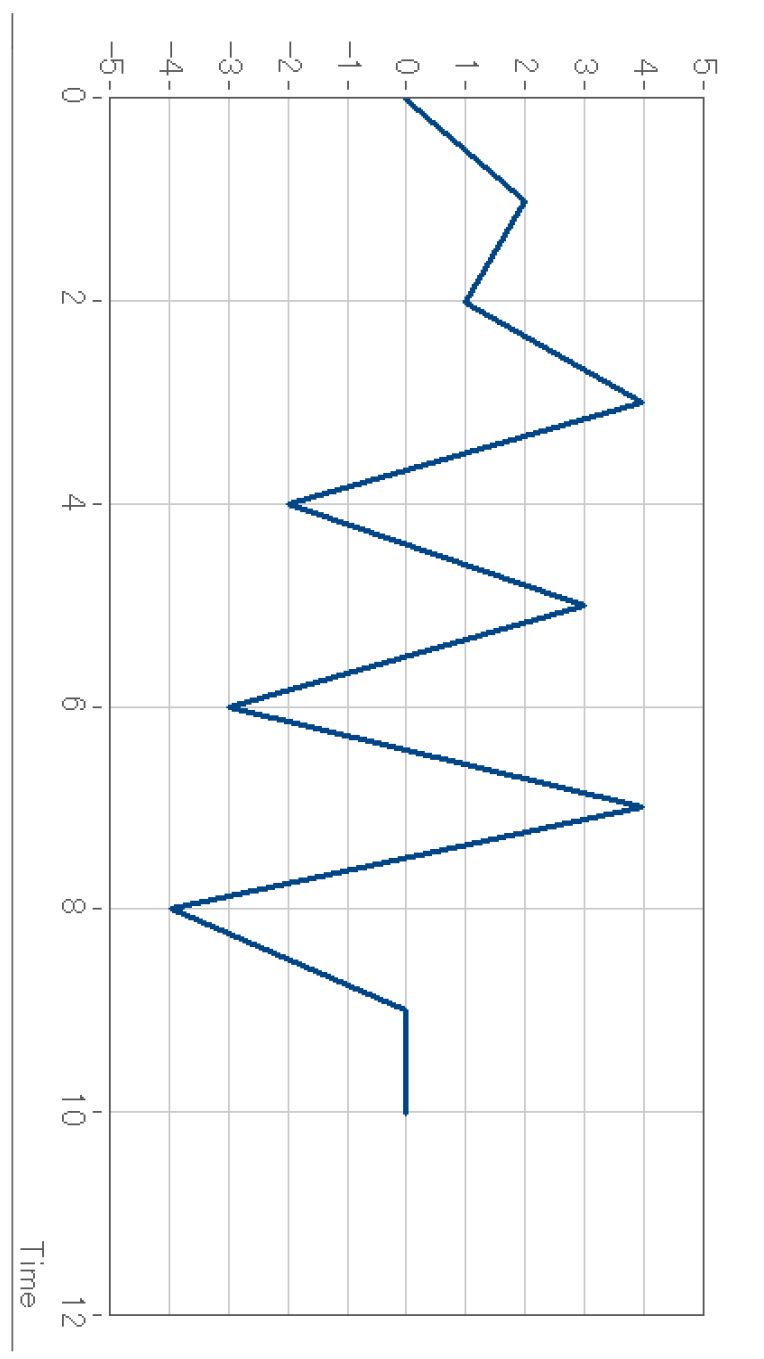
例えば、下図の赤〇、緑〇からのポイントから雨水が流れるとすると、図のような経路を取ることがイメージできます。雨水は、その他すべての極値(尖った点)からも同様に流れていきます。
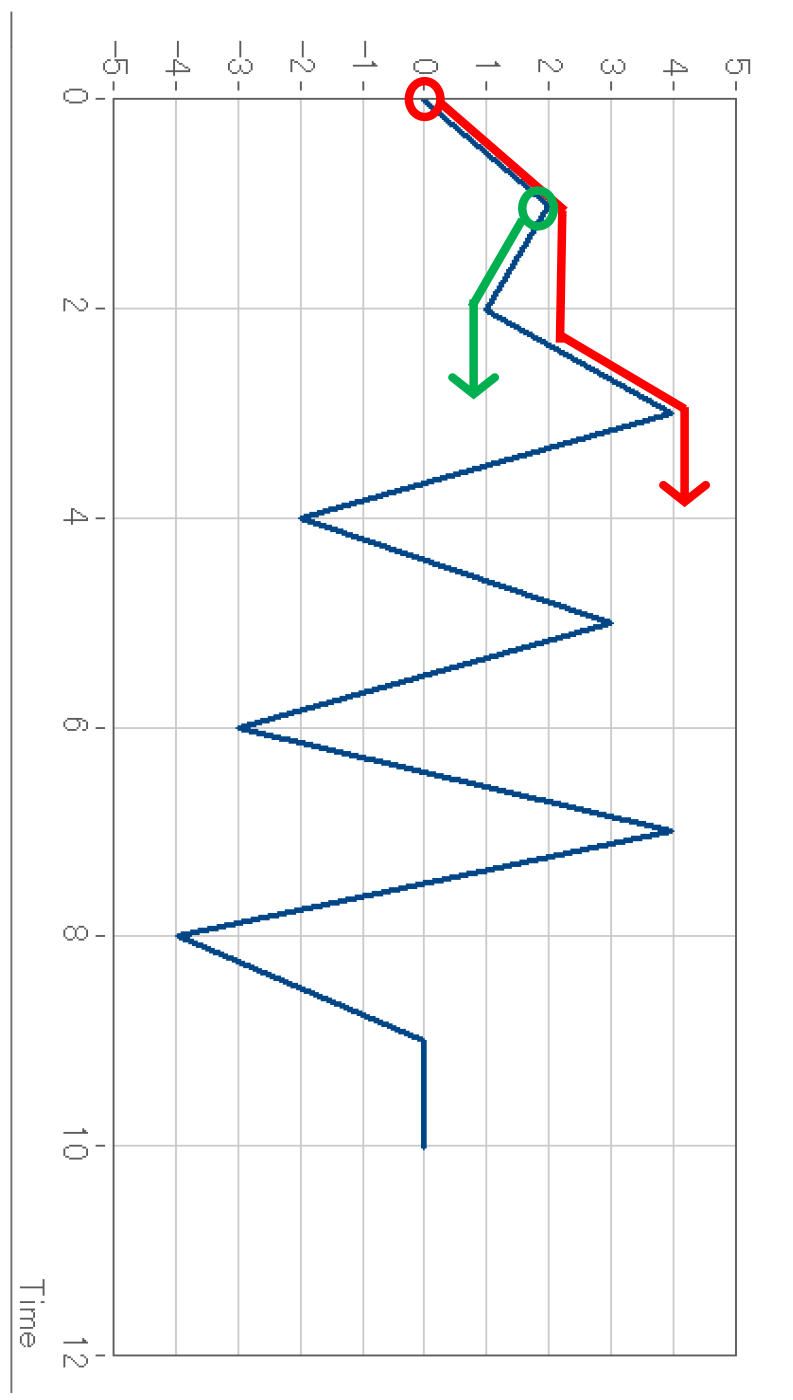
レインフロー法で重要となるのは、一度極値から流れ始めた雨水が、どの点で停止するかです。流れが始まった点、停止した点を使うことで、その経路での振幅を考えることができます。
雨水は、以下の2条件で停止します。
1)流れが右向きである場合、その出発点よりも、もっと左側に次の右向きの出発点がある場合。 (左向きの場合も同様、左右を読み替えて考える)
2)屋根に既に雨水が流れていた場合。
1)流れが右向きである場合、その出発点よりも、もっと左側に次の右向きの出発点がある場合。 の具体例を考えてみましょう。
下図の点Aから流れた雨水は、このような経路を通ったうえでt=4である点で停止します。
これは、点Cが、点Aよりも左側にある、同じく右向きの出発点であるためです。
点Bも右向きの出発点ではありますが、「出発点よりも左側にある」という条件を満たさないため、ここでは停止しません。
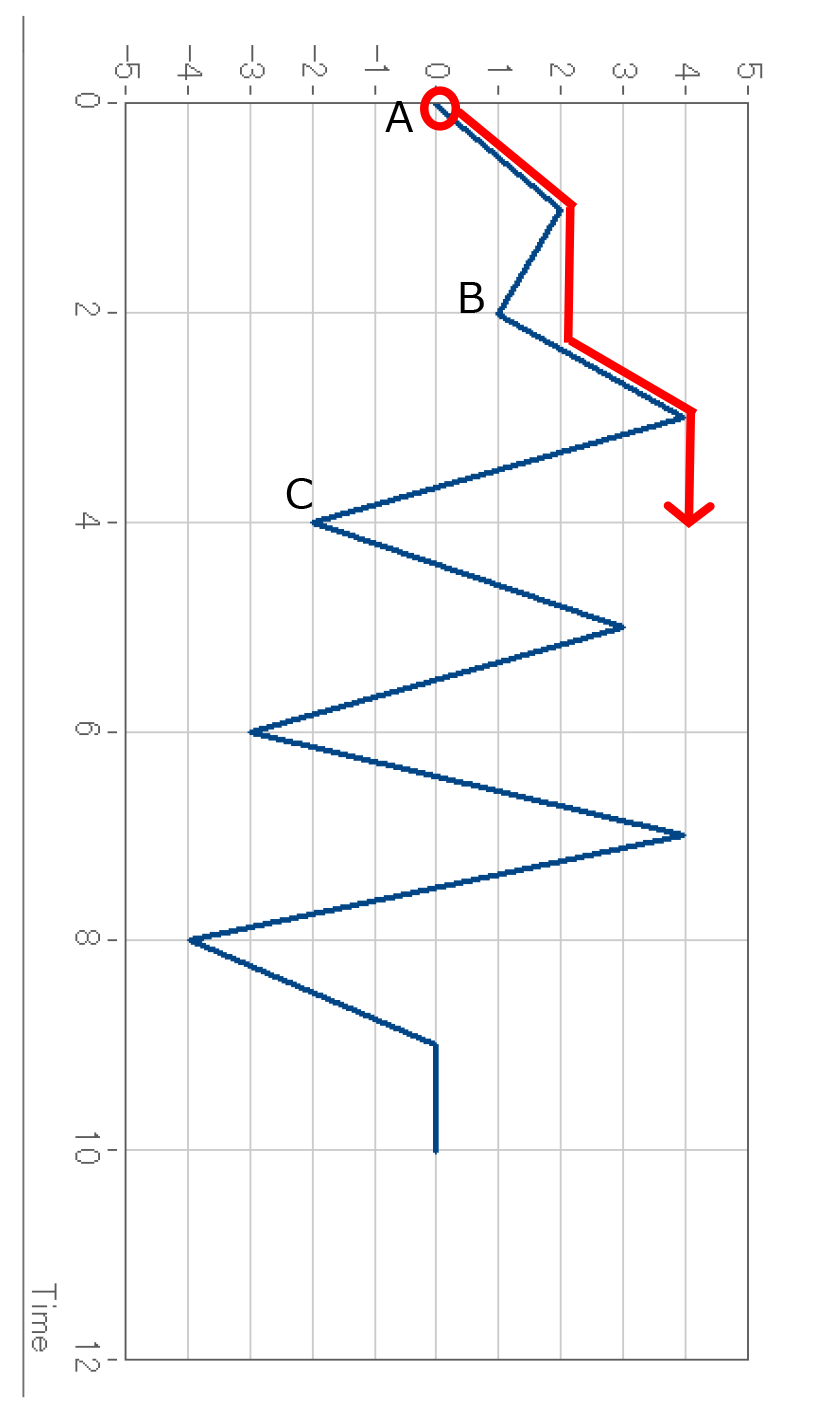
この流れの振幅は、出発点がy=0、停止点がy=4、という情報が使われます。
(実際の解析においてはこれらの値から振幅や平均値を求めます)
2)屋根に既に雨水が流れていた場合。
の具体例を考えてみましょう。
先ほどと同じく、下図の点Aから流れた雨水は、このような経路を通ったうえでt=4である点で停止します。
次に点Bから右向きに流れる雨水を考えると、これはすぐに点Aから流れた雨水とぶつかることになり、「屋根に既に雨水が流れていた場合」の条件を満たして停止します。
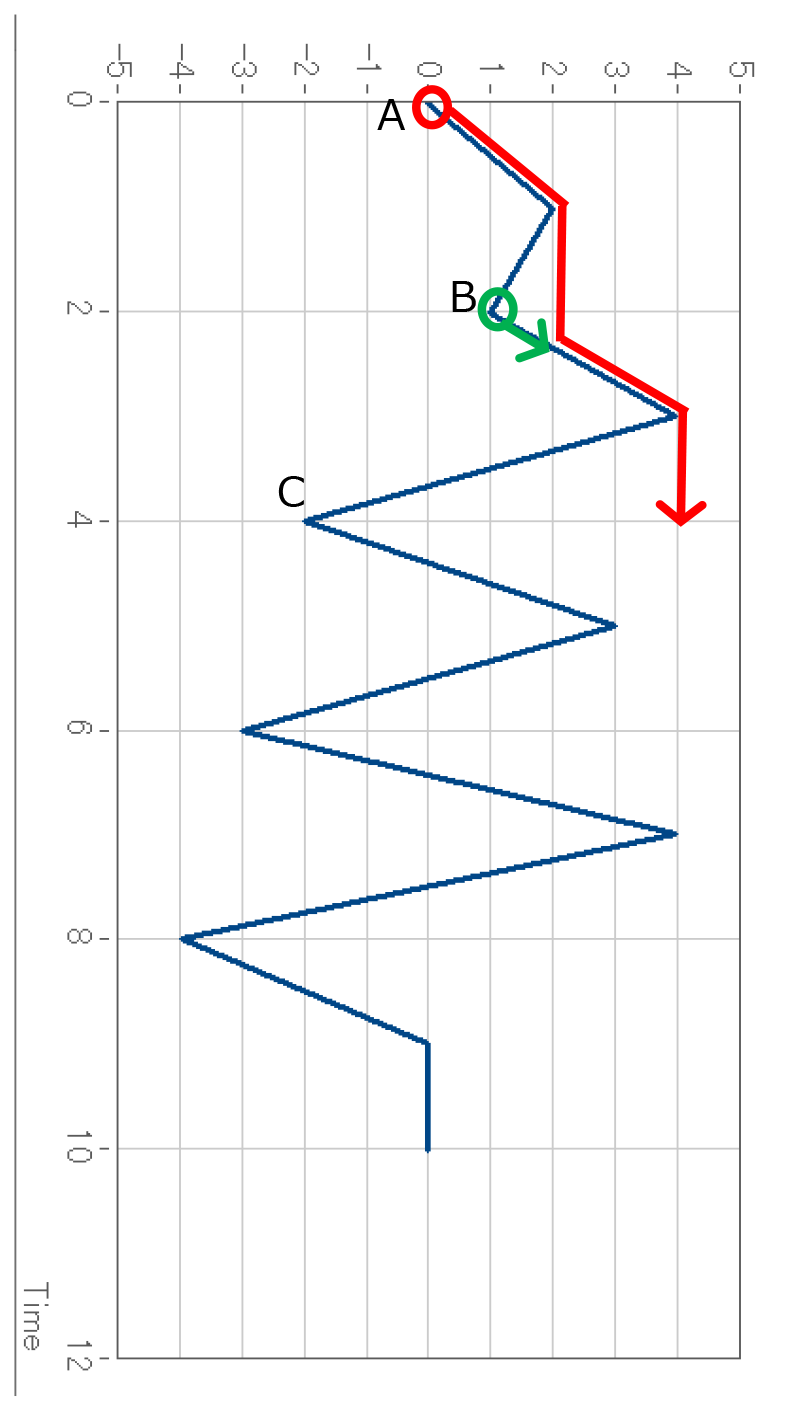
この流れの振幅は、出発点がy=1、停止点がy=2、という情報が使われます。
レインフロー法では、これらの出発点、停止点から「サイクル」という考え方を使います。ある振動が例えばy=0からy=4まで変化したとして、逆向きのy=4からy=0の変化があればそのセットが「1サイクル」です。片方のみの変化があればそれは「ハーフ(1/2)サイクル」として考えられます。
そのため、最終的な結果ではカウントとして0.5という数値が現れることがあります。これは、該当するクラスにおいてハーフサイクルがカウントされたことを意味します。
Qコマンド・関数・キットで同じようなコマンドがありますが、何が違うのですか?
FAQ ID:s034
例えば、ファイル関係に対して以下のようにコマンド・関数・キットとさまざまな方法があります。これらはどのように異なり、どのように使い分ければよいのでしょうか?
| コマンド | B> Load,Save |
|---|---|
| 関数 | 13> ファイル関数 |
| キット | File-kit |

FAMOSの歴史と関係します。概念として以下のような違いがあります。
| コマンド | 非常に簡単に使用できますが、細かなことはできません。 コマンドはFAMOSの古いバージョンで使用していた関数です。 以前のバージョンとの互換性を保つために残されています。 |
|---|---|
| 関数 | 信号処理ソフトウェアとして必要な機能を集約しています。通常はこの関数を利用してください。 |
| キット関数 | 関数でも実現できますが、さらに専門的な処理を実現したものです。 キット関数はアプリケーション使用時のメモリー消費を抑えるために、メニューメニュー”エクストラ/オプション”の”機能拡張/キット関数の登録”で使用するか否か設定可能です。 |
Q複数のグループ変数にある同じチャンネルをまとめたい
FAQ ID:s073
例えば、以下のようにGrp1,Grp2,Grp3があります。この中にch1,ch2,ch3,ch4がそれぞれあります。
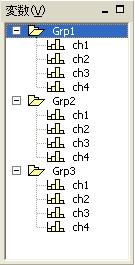
このとき、各グループのch2だけで新しいグループ変数を作成することはできますか?
結果をResultとすれば、以下で実現可能です。
Result:grp1_ch2=Grp1:ch2 Result:grp2_ch2=Grp2:ch2 Result:grp3_ch2=Grp3:ch2
尚、自動処理したい場合には以下のようになります。
i=1 while i<=3 grpname = "Grp"+TForm(i,"F00") resultch = grpname+"_ch2" Result:<resultch>=<grpname>:ch2 i=i+1 end
Q3 温度係数とは何ですか。温度係数はどのように適用されますか。
FAQ ID:セクション I:定義と専門用語
温度が変化すると、マイクロホンの感度に影響が出ることがあります。IEC 61094-4 (計測用マイクロホン) 規格で必要とされる係数は、温度の変動による感度の変化を見積もるために使われます。
詳細情報:
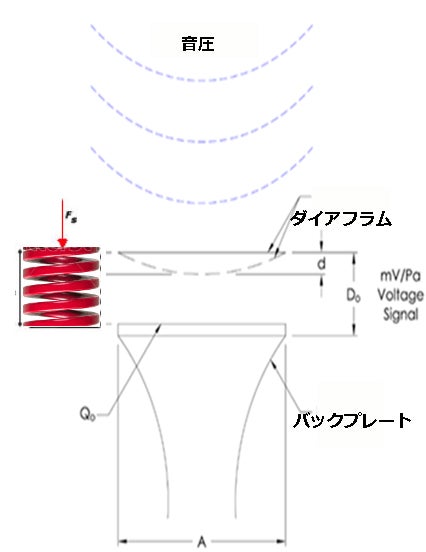
ダイアフラムの堅さと、ダイアフラムとバックプレート間の空隙は、バネのように作用します(下図参照)。温度、湿度、気圧の変化は、上述のバネ効果を変化させ、従ってマイクロホンの感度を変化させます。感度の変化を補正しないと、エンドユーザーが正確に計測しようとしている音圧の計測値が不正確になります。
環境の変化に伴う感度の変化を補正するもっとも良い方法は、しばらく待ってマイクロホンが安定してから、試験環境における正確な感度を携帯型校正器(CAL200等)で計測することです。
携帯型校正器(またはピストンホン)をお持ちでなければ、仕様書にある係数を用いて計算をして、環境の影響を見積もることができます。この例では、気温の変化による感度の変化を補正します。
全ての校正証明書には、オリジナルのマイクロホンの感度と、校正時の環境条件が示されています(下記参照)。

温度係数(下表参照)を用いて、環境影響を加えたり差し引いたりできます。正数であれば、右上がりの傾きを意味します(低温では感度が低く、高温では感度が高くなります)。
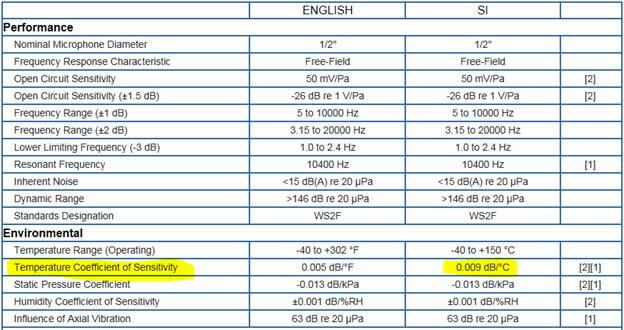
上述の377B02型マイクロホンを使って100℃の環境下で計測する際の感度を計算するには、校正証明書にある温度との差に係数をかけてください。
∆T = 100℃ – 21℃ = 79 ℃ temperature change 79 ℃ * 0.009 dB/℃ = 0.71 dB
377B02型マイクロホンの例では、感度は49.62 mV/Paであり、これは -26.09 dB re 1V/Paに等しくなります。温度変化に伴う感度の変化0.71 dBを-26.09 dBに加算すると、次のような感度が得られます。
0.71 – 26.09 = -25.38 dB re 1V/Pa
新しく求められた-25.38 dB re 1V/Paに、適切な対数換算式を当てはめてmV/Pa単位の感度に換算すると、100℃では53.83 mV/Paというより高い感度が得られます。49.62 mV/Paから53.83 mV/Paへの変化は、直接気温の変化によるものです。
IEC61094-4規格では温度係数は-10℃から+50℃まで求めるよう規定されていますが、PCBでは試験の結果、係数がマイクロホンを使用可能な120℃まで有効であることを確認しました。
QExcel2003がインストールされている場合、Excel形式で出力できません
FAQ ID:g046
Version 4.0 Rev.7までのFAMOSはExcel2003に対応しません。
(Excel2003の方が後から開発されたため。)
Excel2003に対応するためには以下のファイルをダウンロードして、
c:\imc\binに上書きしてください。
Q1/3オクターブのオーバオール値をExcelにコピーしたい
FAQ ID:x169
バージョン3.1からデータのコピーが可能になり、NVGateのグラフデータをExcelにコピーできるようになりました。とても便利です。
ところで、1/3オクターブグラフでコピーすると、オーバオール値がコピーされません。オーバオール値をコピーすることはできるでしょうか?
データのコピーではオーバオール値はコピーされません。
しかし、オクターブマーカを使用すると、オーバオール値をコピーすることができます。
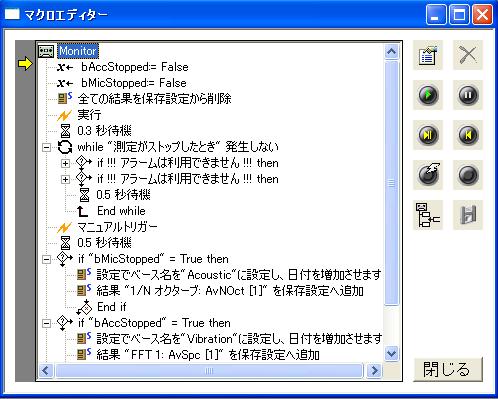
- 1/3オクターブ結果を表示させてください。
- このグラフに"オクターブマーカ"を追加します。
V7以降の場合
表示/グラフタブ>マーカから1/Nオクターブデータを選択します。
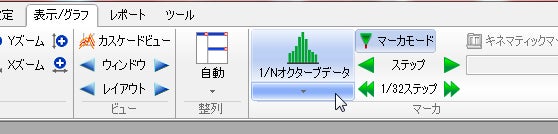 V6以前の場合
V6以前の場合
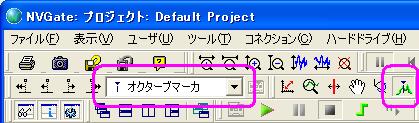
- この結果、インフォトレースにマーカデータが表示されます。
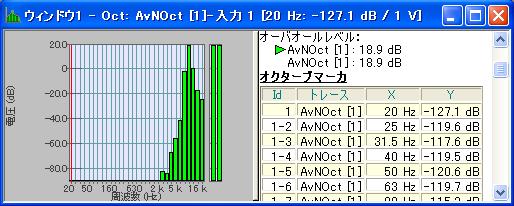
- インフォトレース上で右クリックして、"マーカテーブルをコピー"を選択してください。
以上の方法で、オーバオール値を含んだデータをコピーできます。
QVersion 6.70 リリースノート
Qマクロとは?
QClsPeak2関数(カウント方法、パラメータについて)
カウント方法について
ClsPeak2関数は、ある参照ラインを設定し、そのラインを超えたすべての極値をカウントする、という手法を取ります。
例として下図のデータで、参照ラインとして0の場合を考えます。
ここで「ある参照ラインを設定し、そのラインを超えた」という考え方ですが、極大値の場合は参照ラインよりも上にあること、極小値の場合は参照ラインよりも下にあることを意味します。
つまり、このデータにおいてはy=2の極小値のみはカウントの対象外となります。
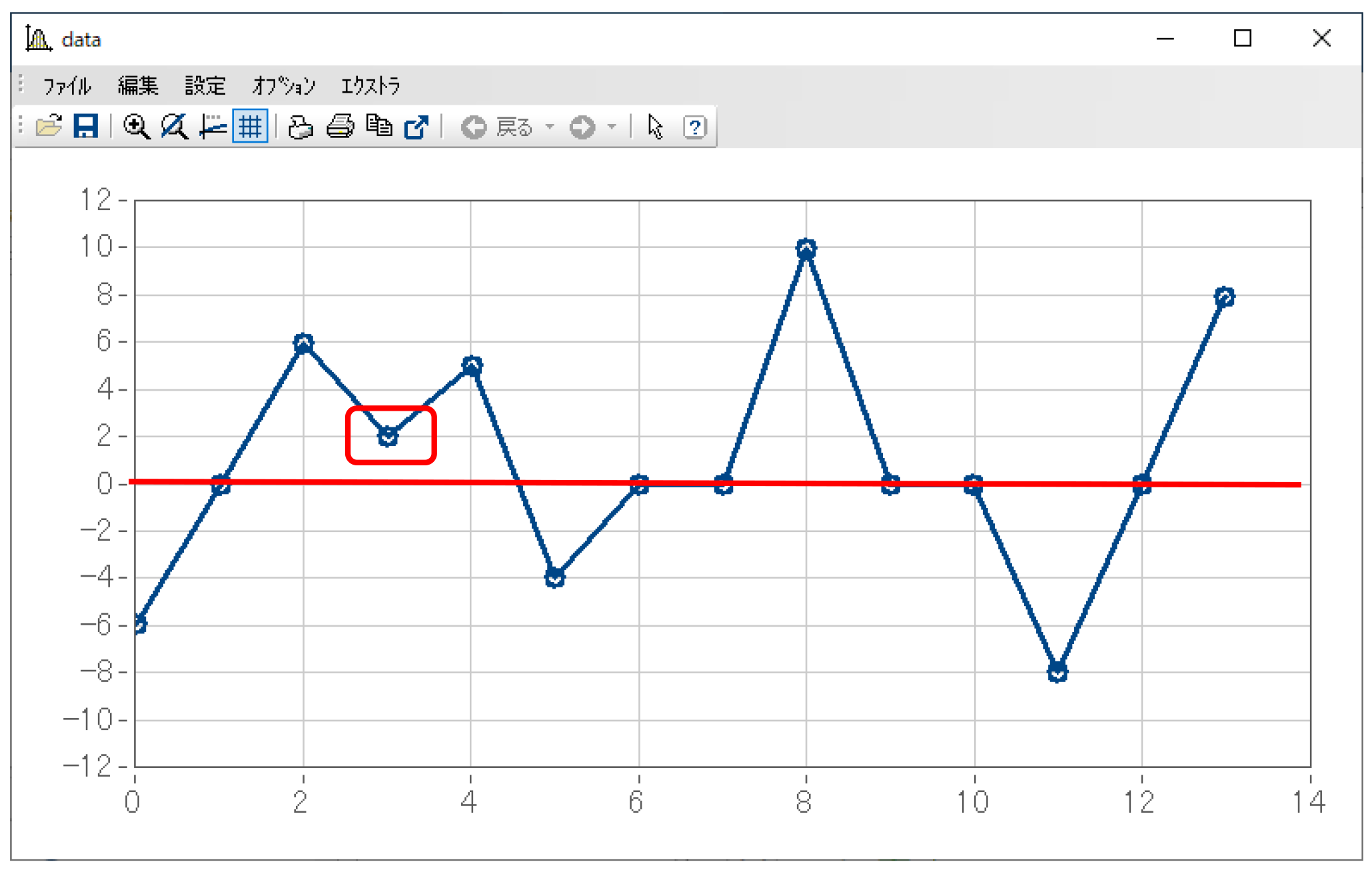
例として参照ラインを3とするなら、このデータにおいてはすべての極大値・極小値がカウント対象となります。
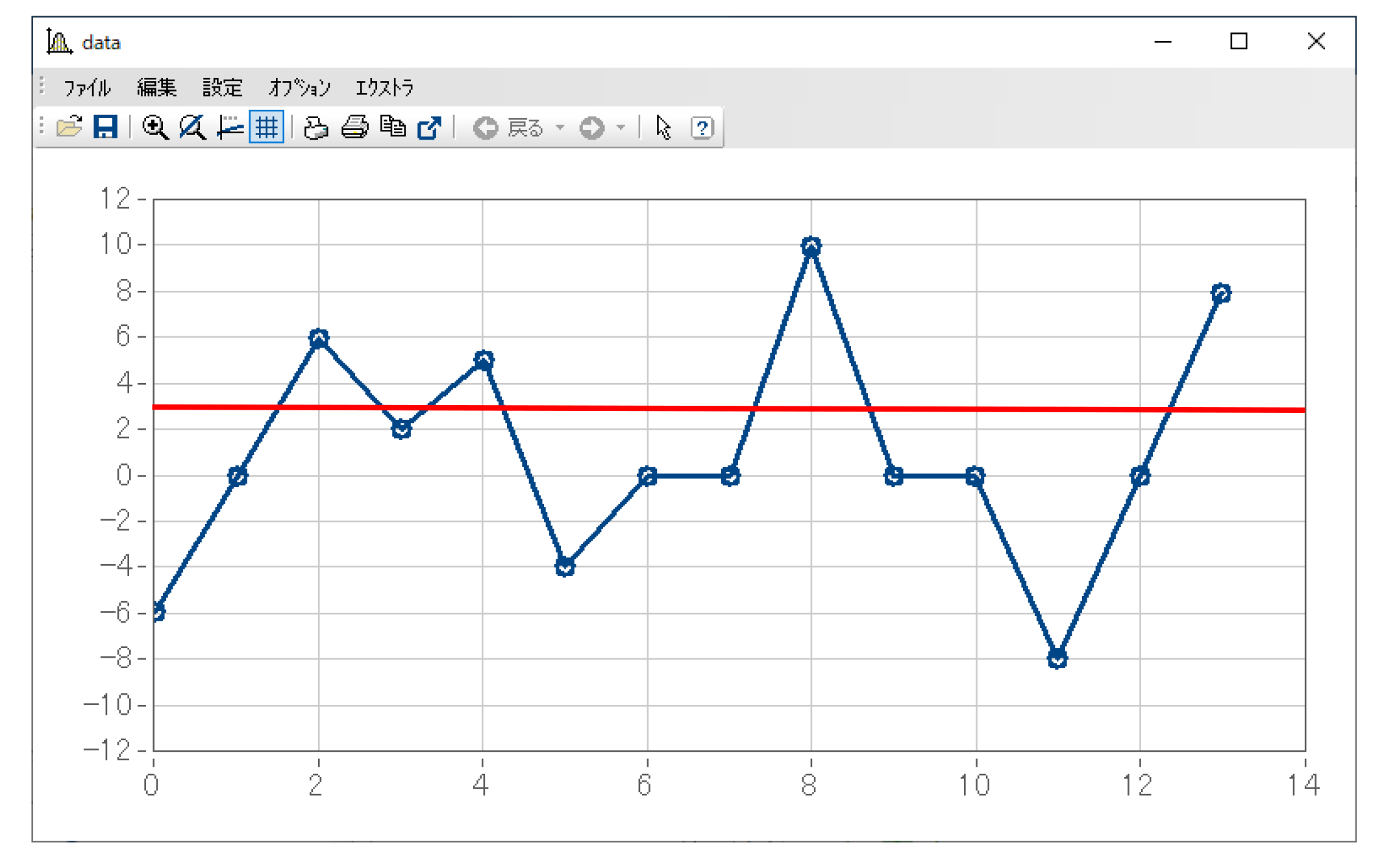
データの始点/終点もカウントの対象となります。
関数のパラメータについて
ClsPeak2関数のパラメータは以下のようになります。 Result = ClsPeak2(data, MaxValue, MinValue, Number of bisn, Reference, Hysteresis, Options)
| Result | カウント結果の変数名 |
|---|---|
| data | カウント対象データの変数名 |
| MaxValue | カウントするレンジの上限 |
| MinValue | カウントするレンジの下限 |
| Number of bins | 分類するクラスの数 |
| Reference | 参照レベル |
| Hysteresis | 小さな振動を無視するためのヒステリシスの大きさ |
| Options | カウントする際の挙動に関するオプション設定 |
Q関数の記述例
レインフロー法は関係する関数が多く、結果の出力方法も何通りか存在します。
まずは基本的な関数の記述例全体をここで述べます。パラメータについては実際の値ではなく_(アンダーバー)付きの名前としています。
; レインフロー法の解析用パラメータの設定
ClsHandle = ClsOffRainflowInit1(_Classes, _UnitUse, _UnitColumn, _UnitRow, _UnitCounter,_Unit_Y_Residue, _SV_0)
ClsOffRainflowInit2(ClsHandle, _Min, _Max, _Hysteresis, _Axes, _Type, _OuterBins, _Calculation)
ClsOffRainflowInit3(ClsHandle, _IgnoreSmallSpans, _Precise, _CountStartEnd, _SV_Null1, _SV_Null2, _SV_Null3)
; 実際にカウント対象となるデータを与える
ClsOffRainflowFeedSamples(ClsHandle, Samples)
; レジデューを結果に加える
ClsOffRainflowAddResidue(ClsHandle, _Weight)
; 結果を返す
RainflowMatrix = ClsOffRainflowGetMatrix(ClsHandle)
; 結果を見やすい形に変換する
ResultRainflow = MatrixSumLines(RainflowMatrix, 0)
関数やパラメータ、変数が多いですが、要点である入力データと解析結果の変数はそれぞれ以下の通りです。
| Samples | カウント対象となる入力データ |
|---|---|
| RainflowMatrix | カウント結果、3次元の配列 |
| ResultRainflow | カウント結果を2次元配列に変換したもの |
クラスカウント法と大きく異なるのは関数の結果の形です。
関数記述例で「結果を返す」「結果を見やすい形に変換する」という箇所が存在する理由を説明します。
例として下図のようなデータを、レインフロー法と、クラスカウント法(ClsPeak2関数)で解析した結果を並べてみます。クラスの分類等、パラメータはなるべく同じように設定しています。
上がレインフロー法の結果(上記の関数記述例ではRainflowMatrixに当たるもの)、下がクラスカウント法の結果です。
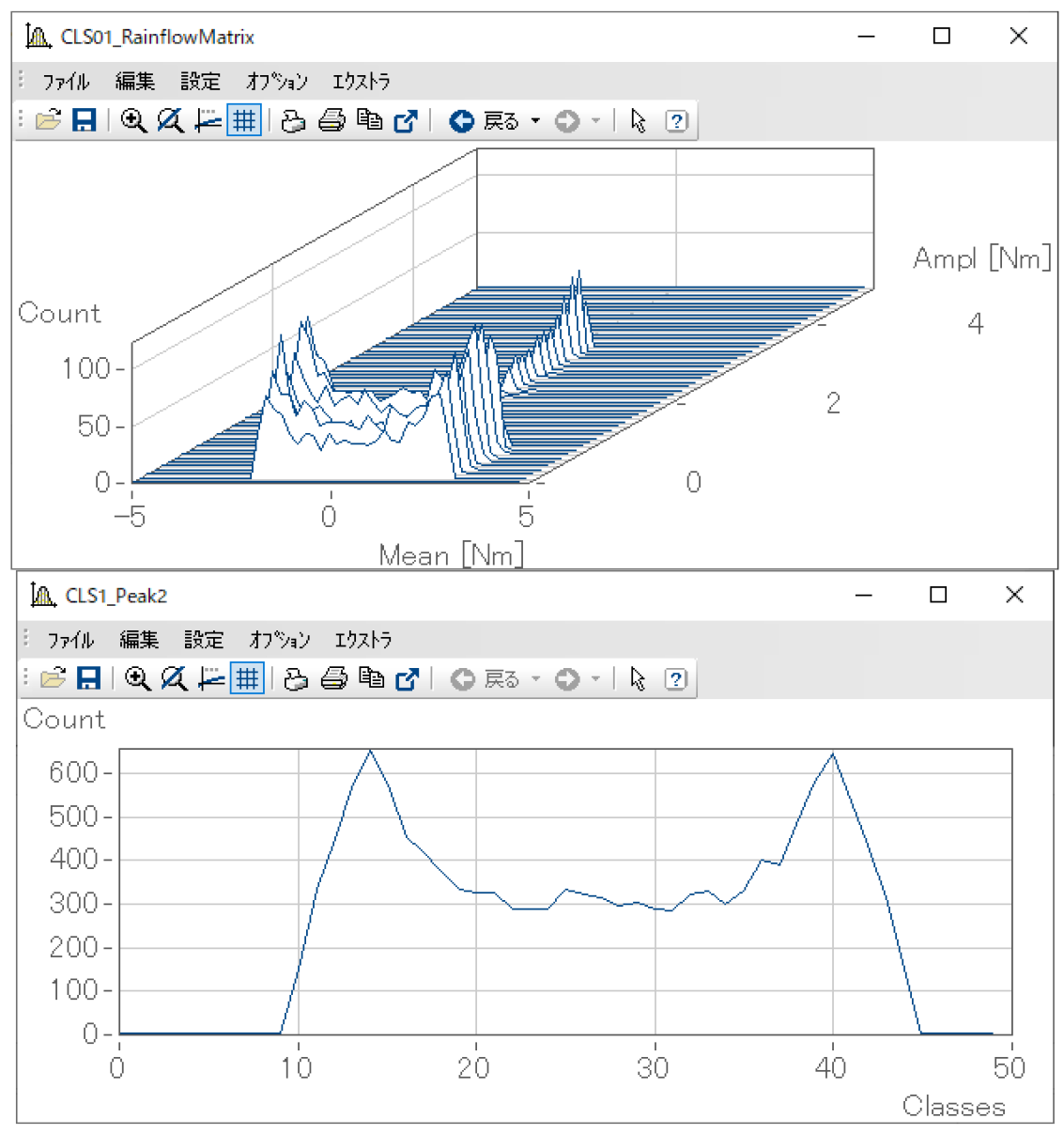
このように、クラスカウント法ではクラスとカウント結果の関係が2次元になるのに対して、レインフロー法では奥行き方向のZ軸も増えて3次元となります。通常、カウントされた後の結果としては2次元である方が後の処理(疲労寿命推定など)で扱いやすいため、関数記述例ではこの3次元から2次元への変換を「結果を見やすい形に変換する」としています。
なお、この図ではX軸はMean(平均)、Z軸はAmpl(振幅)としていますが、これらは関数のパラメータで設定されます。
Qダメージ計算:クラスカウント法向け
クラスカウント法の場合、カウント結果は0から始まるインデックスでクラスに分類されています。例としては下図のような状態です。
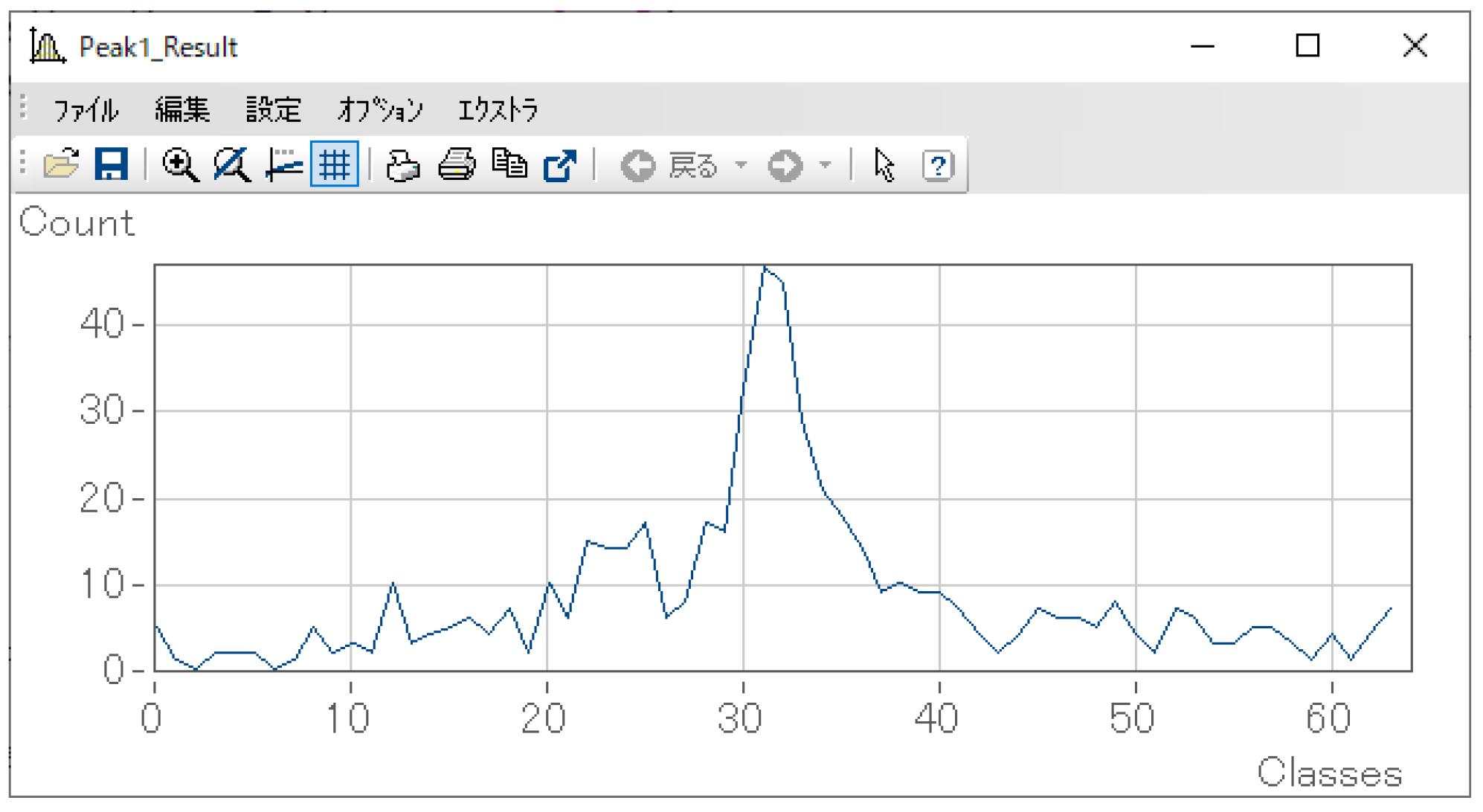
S-N線図では応力Sとして物理単位が使われるため、シーケンスではクラスのインデックスから物理単位に換算して計算を行う必要があります。
ここでは、それぞれ以下の名前を変数として使います。
| SN | S-N線図、応力Sの単位系はクラスカウント法の対象としたデータと同じ |
|---|---|
| Result | クラスカウント法のカウント結果 |
| _MaxValue | カウントしたレンジの上限 (ClsPeak〇関数に使ったパラメータ) |
| _MinValue | カウントしたレンジの下限 (ClsPeak〇関数に使ったパラメータ) |
| _NumberOfBins | 分類されたクラス数 (ClsPeak〇関数に使ったパラメータ) |
| Damage | S-N線図とカウント結果から求められたダメージ |
| TrialTime | 対象データが示す時間、距離など |
| LifeTime | 推定された疲労寿命 |
シーケンスの記述は以下のようになります。
; S-Nを両対数スケール上で検索するために換算
_xlog = Log(SN.X)
_ylog = Log(SN.Y)
; 1クラスのレンジを計算
_range = (_MaxValue - _MinValue) / _NumberOfBins
; すべてのクラスでループ計算
Damage = 0
_i = 1
While _i <= _NumberOfBins
; そのクラスの振幅、応力Sに相当する
_class = Abs(_MinValue + _range * _i)
; 対応する回数NをS-N線図から検索する
_slog = PosiEx(_ylog, Log(_class))
_nlog = Value2(_xlog, _slog, 0)
_N = 10^_nlog
; ダメージに換算する
Damage = Damage + Result[_i] * (1 / _N)
_i = _i + 1
End
; 疲労寿命の推定
TrialTime = 10 ; 対象データ相当の時間/距離などを指定する
LifeTime = TrialTime / Damage
S-N線図が両対数スケールのため、応力Sから回数Nを検索する手順が少々特殊ですが、要点としては「クラスに対応する応力Sを求める」「応力Sに対応する回数Nを求める」「回数Nをダメージに換算して累計を取る」の3点のみです。
QClsPeak3関数(カウント方法、パラメータについて)
カウント方法について
ClsPeak3関数は、すべての極値を、極大値と極小値でそれぞれ別個にカウントする、という手法を取ります。
それぞれ別個に、というのは後述するパラメータの設定に応じて「極大値のみをカウントする」解析モードと、「極小値のみをカウントする」解析モードが存在するということを意味します。
例として下図のデータの場合、パラメータ設定に応じて赤枠で囲った極大値のみをカウントする、または緑枠で囲った極小値のみをカウントする、というどちらかの挙動となります。
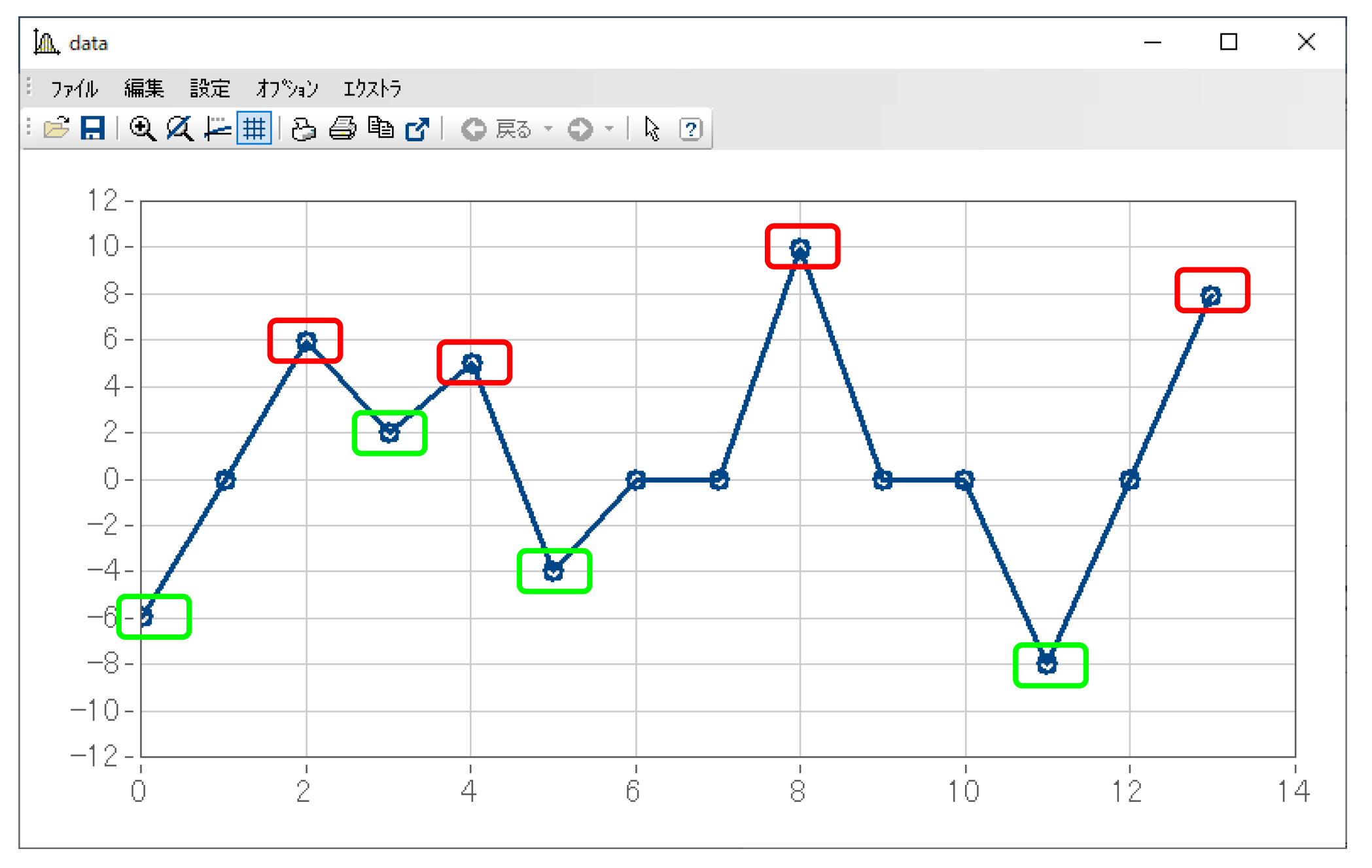
データの始点/終点もカウントの対象となります。始点/終点が極大値/極小値のどちらとしてカウントされるかはデータの形状に依存します。
上図のデータの例では、始点は極小値、終点は極大値として扱われます。
関数のパラメータについて
ClsPeak3関数のパラメータは以下のようになります。
Result = ClsPeak3(data, MaxValue, MinValue, Number of bisn, Hysteresis, Options)
| Result | カウント結果の変数名 |
|---|---|
| data | カウント対象データの変数名 |
| MaxValue | カウントするレンジの上限 |
| MinValue | カウントするレンジの下限 |
| Number of bins | 分類するクラスの数 |
| Hysteresis | 小さな振動を無視するためのヒステリシスの大きさ |
| Options | カウントする際の挙動に関するオプション設定 |
Optionsはオプション設定用の値で、以下の4つが存在します。
0:極大値のみをカウントします。
1:クラスの上限/下限の外にあるデータもカウントの対象とし、極大値のみをカウントします。
例えば、クラスの上限が8でy=10の極値がある場合、この極値は上限のクラスに含まれるものとしてカウントします。逆にoptions=0の場合はこの極値は無視されます。
2:極小値のみをカウントします。
3:クラスの上限/下限の外にあるデータもカウントの対象とし、極小値のみをカウントします。
極大値も極小値もすべてカウントする、という使い方をしたい場合は、Optionsの0または1でカウントした結果と、Optionsの2または3でカウントした結果を合算することで求めることができます。
QClsOffRainflowInit1 関数
ClsOffRainflowInit1関数は、レインフロー法の解析用パラメータを設定するための関数の1つです。パラメータは以下のようになります。
ClsHandle =ClsOffRainflowInit1(_Classes, _UnitUse, _UnitColumn, _UnitRow, _UnitCounter, _Unit_Y_Residue, _SV_0)
| ClsHandle | 以後の関数群が参照するための変数 (名称は任意) |
|---|---|
| _Classes | クラス数をいくつにするかの設定、4以上1000以下 |
| _UnitUse | クラス幅をどのようにスケーリングするかの設定 0:クラス番号でスケーリング(0, 1, 2...) 1:入力データ自体の物理単位でスケーリング |
| _UnitColmn | 結果のX軸の単位 (X軸の意味は後述) |
| _UnitRow | 結果のZ軸の単位 (Z軸の意味は後述) |
| _UnitCounter | 結果のY軸の単位 (Y軸はカウント回数) |
| _Unit_Y_Residue | レジデューのY軸の単位 (基本的にカウント回数) |
| _SV_0 | 常に0に設定しておく現在は使われていないパラメータ |
〇軸の単位、というパラメータは表記上の文字列の設定です。
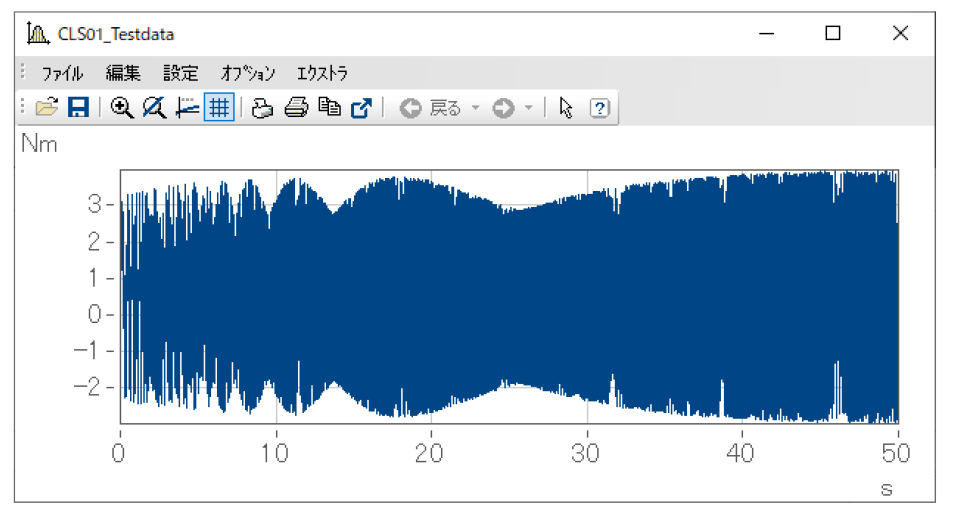
例えば下図の結果の場合、X軸の単位はMean [Nm]、Z軸の単位はAmpl [Nm]、Y軸の単位はCountという文字列がそれぞれ設定されています。ここでのX軸、Z軸の設定はあくまで表記上の文字列のみであり、実際の軸の意味自体はClsOffRainflowInit2関数で設定します。
クラス幅のスケーリング、_UnitUseは1、つまり入力データ自体の物理単位によるスケーリングが使用されています。
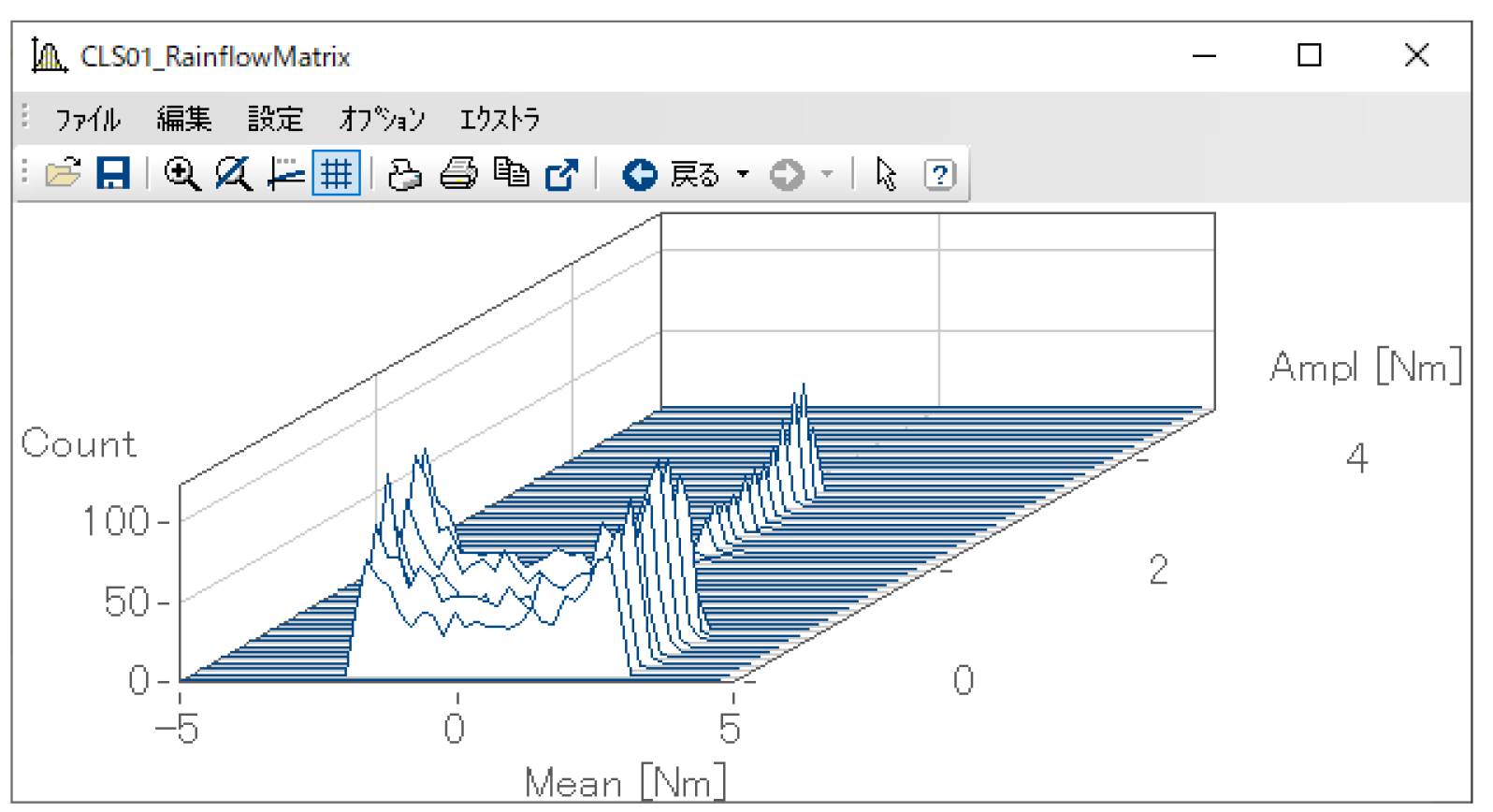
これ単体では解析用パラメータの設定は完結せず、ClsOffRainflowInit2、ClsOffRainflowInit3関数へ続きます。続く関数では、この関数で作成される変数であるClsHandleを参照します。
Qダメージ計算:レインフロー法向け
レインフロー法の場合、専用の関数が存在しており簡単な記述で疲労寿命推定を行うことができます。
ここでは、それぞれ以下の名前を変数として使います。
| SN | S-N線図、応力Sの単位系はレインフロー法の対象としたデータと同じであり、レンジ(振動の最大値-最小値)でスケールが記述されている必要があります。 |
|---|---|
| ClsHandle | ClsOffRainflowInit1関数で作成された変数(データを与えカウントまで完了していること) |
| Damage | S-N線図とカウント結果から求められたダメージ |
| TrialTime | 対象データが示す時間、距離など |
| LifeTime | 推定された疲労寿命 |
シーケンスの記述は以下のようになります。
; ダメージ計算、後ろ2つのパラメータは任意に指定する
Damage = ClsOffWoehlerSN(ClsHandle, SN, _ClassRelation, _Interpolation)
; 疲労寿命の推定
TrialTime = 10 ; 対象データ相当の時間/距離などを指定する
LifeTime = TrialTime / Damage
ClsOffWoehlerSNのパラメータが示す意味は以下の通りです。
ClsOffWoehlerSN(ClsHandle, SN, _ClassRelation, _Interpolation)
| ClsHandle | ClsOffRainflowInit1関数で作成された変数 |
|---|---|
| SN | S-N線図 |
| _ClassRelation | カウントのクラスは実際には幅があるが、その幅の中でどの程度の応力と見積もるかの設定 0:クラス全体の範囲で等しく分布していると考えます 1:クラスの最大値であると考えます (=最もダメージが大きくなる) 2:クラスの中間点であると考えます |
| _Interpolation | S-N線図の補間の仕方 0:S-N線図は両対数スケールとして補間する 1:S-N線図は応力Sがリニア、回数Nが対数スケールとして補間する |
Q0056のように0付の番号でファイル名・フォルダ名を生成したい。
FAQ ID:s071
番号順にデータを保存したいと考えていますが、1,2,3..のように並べると、エクスプローラで見たときに1,10,11...のように順番が異なってしまいます。
0056のように0をつけると順番に並ぶのでそのように出力したいです。
回答以下のシーケンスで対応可能です。
以下のシーケンスはサブシーケンスとして作成しています。
Sequence CreateNumberString "56", 4, result
と呼び出すと、"0056"がresultに出力されます。
;_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/
;
; 0付の番号ファイル名 [0046] を生成します
;
;_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/
; 引数
;----------------------------------------------------------------
_k2_numstr = PA1 ;数字の文字列を指定します
_k2_digit = PA2 ;桁数
; Example
; _k2_numstr = "56"
; _k2_digit = 4
_k2_number = TtoSv(_k2_numstr, "F")
_k2_temp=""
_k2_cnt=1
while _k2_cnt<=_k2_digit
if _k2_number <= 10^(_k2_digit-_k2_cnt)-1
_k2_temp = _k2_temp+"0"
end
_k2_cnt=_k2_cnt+1
end
_k2_result = _k2_temp+TForm( _k2_number, "F00")
;戻り値
;----------------------------------------------------------------
PA3 = k2_result ;文字列
;変数のクリーンナップ
;----------------------------------------------------------------
Delete _k2_*
Qパルス波形を分周するためにはどうすればよいですか?
FAQ ID:s030
パルス波形を分周する関数は存在しません。シーケンスで作成します。
下記サンプルを参考にしてください。
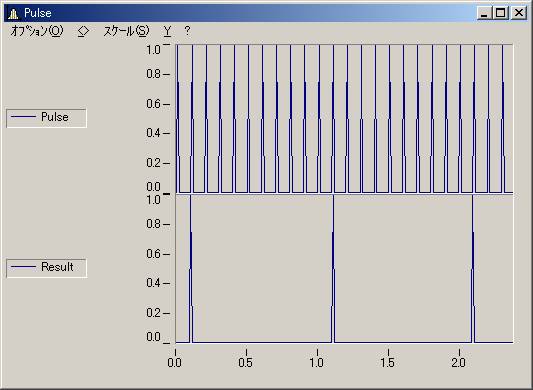
;************************************************************ ; パルス波形を分周するサンプル ;************************************************************ ;------------------------------------------------------------ ; サンプルデータを作成します ;------------------------------------------------------------ _xdelta = 0.01 _xpoint = 1000 _temp1 = Ramp( 0, _xdelta, _xpoint) _temp2 = Ramp( _xdelta, _xdelta*10, _xpoint/10) Pulse = Set( _temp1*0, _temp2, _temp2*0+1) Delete _* Show Pulse ;//////////////////////////////////////////////////////////// ; データ処理部 ; パルス波形を1/10に分周します ;------------------------------------------------------------ ;【引数】 ; Pulse = 入力データ ; ;【戻値】 ; Result = 結果 ; ;【パラメータ】 _Ratio = 10 ;//////////////////////////////////////////////////////////// ;各パルスを取得します。 ; 本サンプルではパルス形状は台形ではなく、インパルス状ですが ; いずれにも対応します。 _ckLevel = SearchLevel(Pulse, 2, 0.5, 0, 2, 0, 0, 1) _ckLevel.Y = _ckLevel.Y*0+1 ;分周するために各パルスにラベルをつけます _Counter = Int( _ckLevel.Y) _Counter = Leng( _Counter, Leng?(_Counter)-1) _Divider = Mod( _Counter, _Ratio) _Divider = XYof( _ckLevel.X, _Divider) ;指定(分周)されたパルスを取得します。 _DivLevel = SearchLevel( _Divider, 3, 1, 1, 2, 0, 0, 1) Result = Set( Pulse*0, _DivLevel.X, Leng(0,Leng?(_DivLevel))+1) ;//////////////////////////////////////////////////////////// ;結果を表示します CvYAxis( Pulse, Result, 0,0,0, 400, -2) CvAttrib(Pulse, 1)