ソフトウェアをアップデートするためにインストールを行っています。最初に既存のアプリケーションを削除するように選択しましたが、コントロールパネルから削除するようにメッセージが表示されます。

FFTアナライザ制御ソフトウェアの”NVGate” Version 2.3よりインストーラを変更しました。

従来はWindowsインストーラを使用してたのでインストーラを起動すると、既にFFTアナライザ制御ソフトウェア”NVGate”がインストールされていた場合には削除するように指示され、再度、インストーラを起動してインストールを行っていました。 

Version 2.3からはNVGateがインストールされているかどうか自動でチェックして、インストールされていた場合には自動で削除します。 

但し、Windows2000 SP4、WindowsXP SP1より前のバージョンをご使用になっている場合には自動で削除することができず、コントロールパネルから削除するようにメッセージが表示され、終了します。 

この場合、”コントロールパネル/プログラムの追加と削除からNVGateを削除してください。

製品詳細はこちら

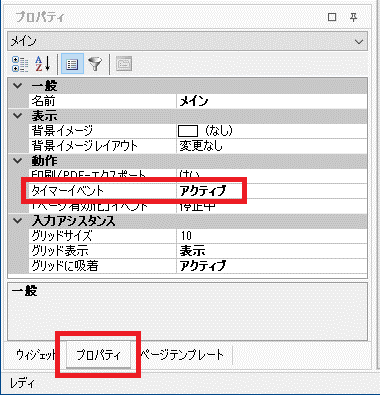
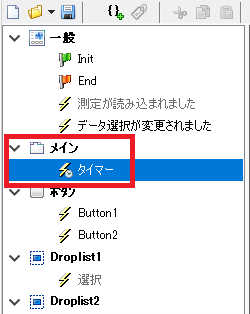
パネルのタイマー機能の使用例を紹介するサンプルパネルを用意しました。

FAMOSでサンプルパネルを読み込んで実行してください。
変数リストの[測定]タブで波形を1つ選択してください。

タイマーはパネルの[プロパティ]＞[タイマーイベント]を"アクティブ"にすることにより、デザインモード時に[コード]に"タイマー"が追加されます。

製品詳細はこちら

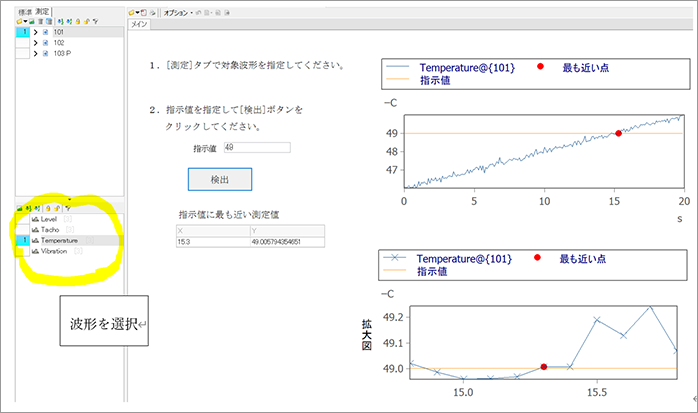
指定した値に最も近い実測値を検出するサンプルパネルを用意しました。

FAMOSでサンプルパネルを読み込んで実行してください。
変数リストの[測定]タブで波形を1つ選択してください。
[指示値]に数値を入力後、[検出]ボタンをクリックしてください。波形から指定した値に最も近い実測値を検出し、[指示値に最も近い測定値]表へ出力します。
また、右下のカーブウィンドウに検出した点付近を拡大した波形を表示します。

製品詳細はこちら

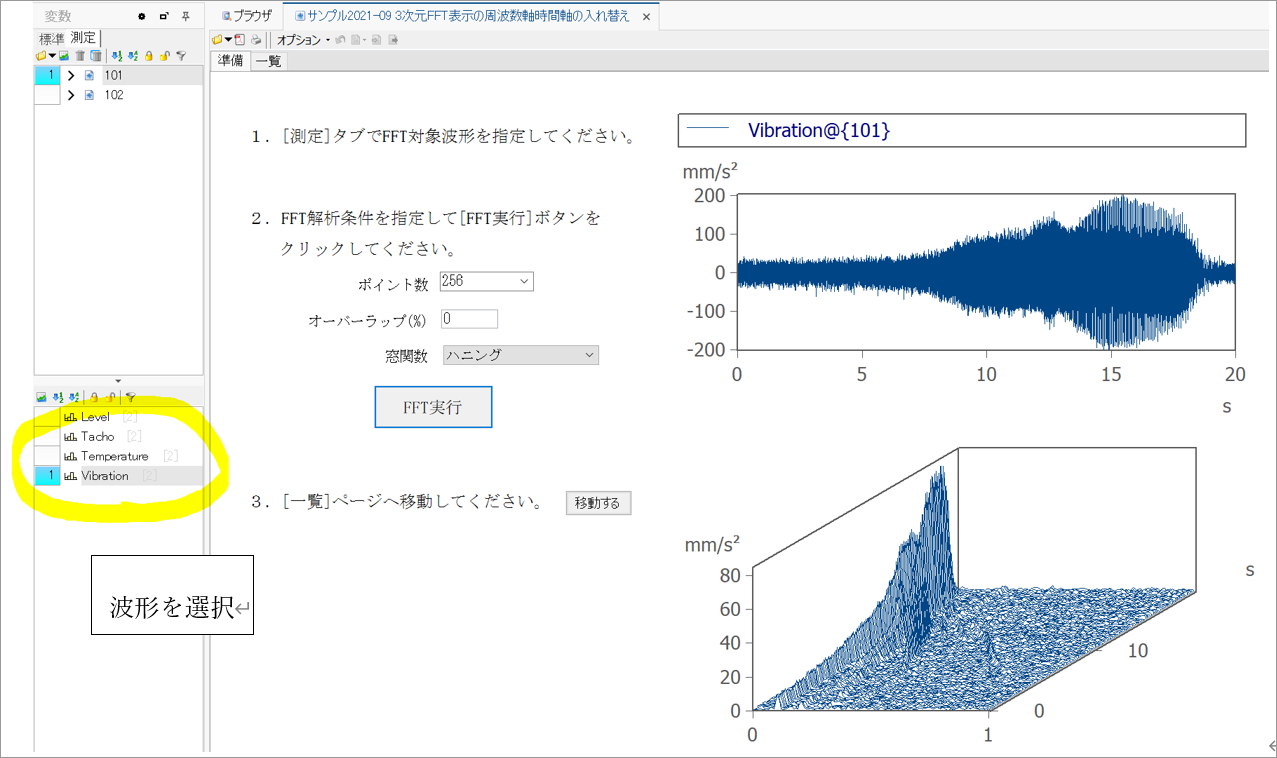
3次元FFT表示の周波数軸と時間軸を入れ替えたカーブウィンドウを表示するサンプルパネルを用意しました。

FAMOSでサンプルパネルを読み込んで実行してください。
変数リストの[測定]タブで波形を1つ選択してください。
[準備]タブで[FFT実行]後、[移動する]ボタンをクリックしてください。
[一覧]タブの上側に横軸周波数、奥行き軸時間の標準の表示、下側に横軸時間、奥行き軸周波数と軸を入れ替えたカーブウィンドウを表示します。
3次元FFT結果はMatrixTranspose()関数で周波数軸と時間軸の入れ替えができます。

製品詳細はこちら

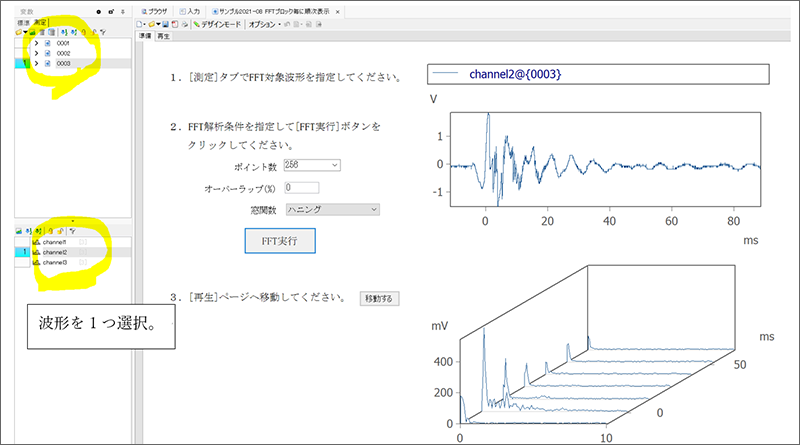
FFT処理結果をFFTブロック毎に順次表示するサンプルパネルを用意しました。

FAMOSでサンプルパネルを読み込んで実行してください。
変数リストの[測定]タブで波形を1つ選択してください。
[準備]タブで[FFT実行]後、[再生]タブの[開始する]ボタンをクリックしてください。左下のカーブウィンドウにFFTブロックを1つずつ抜き出して表示します。
表示間隔(秒)のデフォルト値はFFTブロック間の時間間隔になります。表示間隔は任意の時間に設定可能です。

製品詳細はこちら

媒介変数表示されたX、Y波形からXYof()関数によりXY波形を作成してください。

例)
_a = 2
_turns = 3
_theta = ramp(0, 0.01, 100*_turns +1)*PI2
_x = _a * ( cos(_theta) + _theta * sin(_theta) ) - _a
_y = _a * ( sin(_theta) - _theta * cos(_theta) )
{インボリュート} = XYof(_x, _y)

製品詳細はこちら

RPM波形上で指定した時間での振動などの波形のFFT結果を抜き出して表示するサンプルパネルを用意しました。

FAMOSでサンプルパネルを読み込んで実行してください。
変数リストの[測定]タブでRPM波形とFFT処理を行う波形をそれぞれ1つ選択してください。
[準備]タブでFFT処理を適用したのち、[確認]タブでFFT結果を見たい時間をRPM波形で指定してください。
ウォーターフォール表示されたFFT結果から指定した時間のFFT結果を抜き出して右下のカーブウィンドウに表示します。

付属のRPMフォルダーはサンプルデータになります。
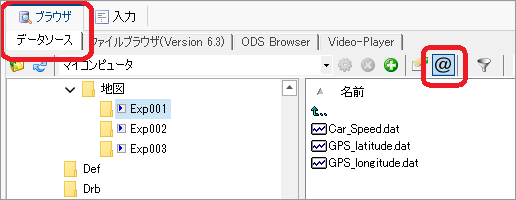
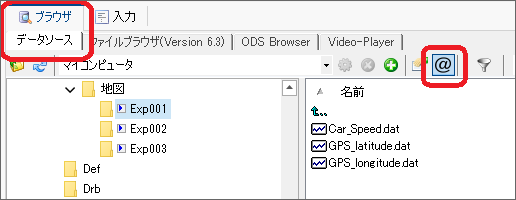
[ブラウザ]＞[データソース]タブにて[＠]を有効にした状態で読み込んでください。

製品詳細はこちら

異常値が最大値から5%、最小値から5%の範囲に収まるような、言い換えると5%から95%の値の範囲での平均を求める場合は、下記のようなシーケンスで求めることができます。

例)
Load slope
_data = slope ; サンプルデータ

_sort = Sort(_data, 1)
_pt = Leng?(_data) ; データ点数
Mean5%to95% = Mean(CutIndex(_sort, _pt * 0.05, _pt * 0.95)) ; 5%～95%区間での平均

製品詳細はこちら

フリーウェアなどで音声部を.wavファイルとして取り出してからFAMOSへ読み込んで下さい。

製品詳細はこちら

緯度・経度波形から走行軌跡を描画するサンプルパネルを用意しました。

FAMOSでサンプルパネルを読み込んで実行してください。
変数リストの[測定]タブで波形を3つ(緯度・経度、車速etc.)選択してください。
緯度・経度波形から走行軌跡を描画するとともに、車速等の波形をカラーパレットとして走行軌跡に情報を付加します。

付属のExp001フォルダーはサンプルデータになります。
[ブラウザ]＞[データソース]タブにて[＠]を有効にした状態で読み込んでください。

製品詳細はこちら

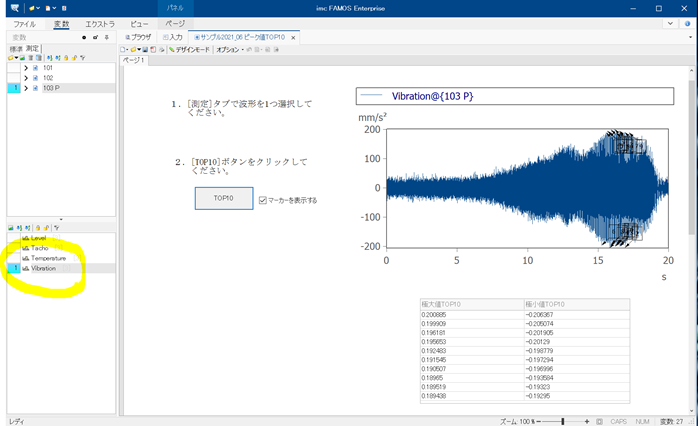
ピーク値(極大値・極小値)のTOP10を表示するサンプルパネルを用意しました。

FAMOSでサンプルパネルを読み込んで実行してください。
変数リストの[測定]タブで波形を1つ選択してください。
小さな凹凸も極小値・極大値であるため、検出対象になります。波形に小さな凹凸が多くある場合はSMO()関数、FiltLP()関数などでスムージング処理を事前に行っておくことをお勧めします。

製品詳細はこちら

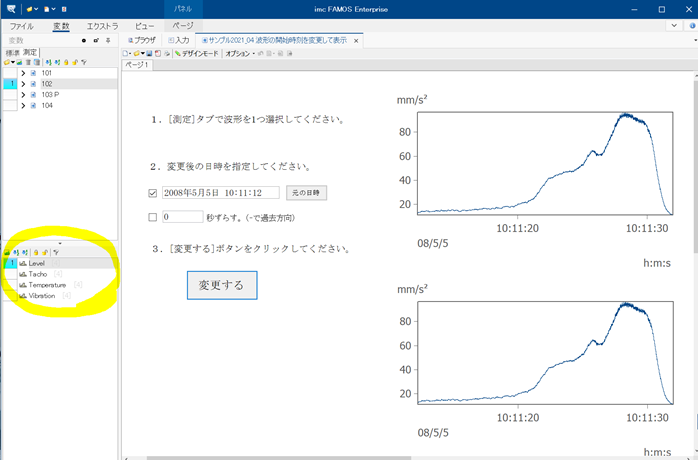
波形の開始時間(絶対時間)を変更するサンプルパネルを用意しました。
FAMOSでサンプルパネルを読み込んで実行してください。
変数リストの[測定]タブで波形を1つ選択してください。項2で指定した日時を波形の[作成]プロパティに設定することにより波形の開始時間を変更します。
 

製品詳細はこちら

FAMOSでは波形(配列)から単数値を引くことで波形全体に対しての減算となります。
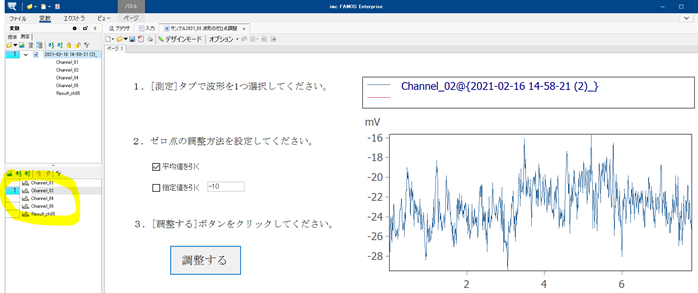
一定値または平均値を引くことでゼロ点を調整するサンプルパネルを用意しました。
FAMOSでサンプルパネルを読み込んで実行してください。
変数リストの[測定]タブで波形を1つ選択してください。項2で指定された方法でY値のゼロ点を調整して表示します。
 

製品詳細はこちら

媒介変数表示されたX、Y波形からXYof()関数によりXY波形を作成してください。

例)
_a = 2
_theta = ramp(0, 0.01, 100+1)*PI2
_x = _a * (1+ cos(_theta)) * cos(_theta)
_y = _a * (1+ cos(_theta)) * sin(_theta)
{カージオイド} = XYof(_x, _y)
 

製品詳細はこちら

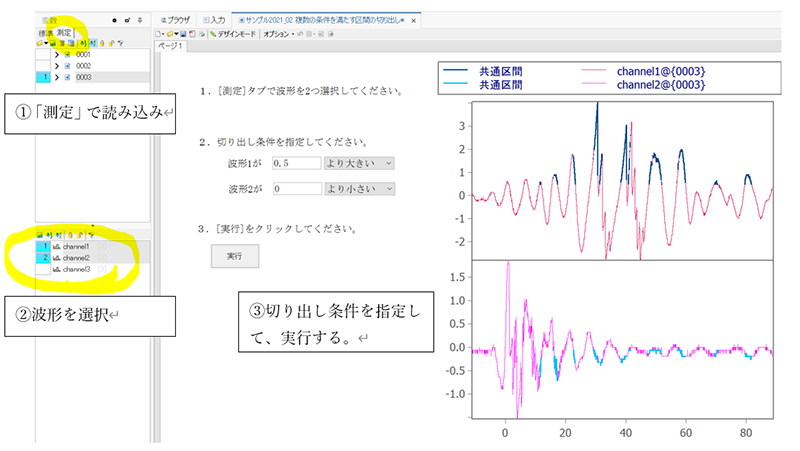
2つの波形で条件を満たす区間を表示するサンプルパネルを用意しました。
FAMOSでサンプルパネルを読み込んで実行してください。
変数リストの[測定]タブで波形を2つ選択してください。選択した2つの波形について、指定した条件を満たす区間が重複する区間を表示します。
使用例1) 波形1の値が1以上かつ波形2の値が3以下 の区間
使用例2) 速度が50km/h以上かつギアが5 の区間
 

製品詳細はこちら

文字列"This is a blue pen. That is red pen."から"is"を検索して、その位置を返します

Result = TxWhere( "This is a blue pen. That is red pen.", "pen")

結果は 6 となります。
検索する文字列が複数ある場合、最初に見つかった位置だけが返されます。 文字列が見つからなかった場合、0が返されます。

製品詳細はこちら

関数”DlgSetText”関数を使用してください。

DlgSetText("Label1","ラベル１")

製品詳細はこちら

FileName?()関数を使用して下さい。

製品詳細はこちら

Sort()関数で並べかえ後、50%目のインデックスでの値が中央値になります。第1四分位数、10%値等も同様に求めることができます。

例)
Load slope
_data = slope ; サンプルデータ

_sort = Sort(_data, 1)
_pt = Leng?(_data) ; データ点数
Median = _sort[_pt * 0.5] ; 中央値
FirstQuartile = _sort[_pt * 0.25] ; 第1四分位数
ThirdQuartile = _sort[_pt * 0.75] ; 第3四分位数
InterquartileRange = ThirdQuartile - FirstQuartile ; 四分位範囲
{10percentile} = _sort[_pt * 0.1] ; 10%値
{90percentile} = _sort[_pt * 0.9] ; 90%値

製品詳細はこちら

• Rectangular
• Hanning
• Hamming
• Blackmann
• Blackman-Haris
• Flat-Top

各ウィンドウは様々な特性を持っています。ウィンドウを選択する際には信号の周波数特性を予め把握しておく必要があります。信号が対象とする周波数から離れた周波数に強いノイズを含む場合、高いサイドローブの傾きが必要になります。

信号が様々な信号から構成され互いに接近している場合、スペクトラム分解能が重要になります。この場合、狭いメインローブを選択するとよいです。信号の振幅が重要な場合には広いメインローブを選択してください。信号が広い周波数範囲に存在する場合にはRectangularを使用してください。一般的にHanningは95%程度のアプリケーションに対応します。

Flat-Topは良い振幅特性を表します。しかし、メインローブが広いので分解能・漏れの特性が良くありません。

インパクトなどの過渡的な信号を解析する場合には、ウィンドウを使用しないほうが良いです。ウィンドウを使うとサンプルの最初で重要な情報が欠落してしまいます。代わりにForce、Exponentialを使用してください。

アプリケーション

• 正弦波・正弦波の集合 Hanning
• 正弦波（振幅特性を重視） Hamming
• 狭帯域ランダム信号 Hanning
• 広帯域ランダム信号 Rectangular
• 近接した正弦波 Rectangular・Hamming
• 加振信号（ハンマー加振） Force
• 応答信号 Exponential
• 未知の信号 Hanning

ウィンドウ関数について

A0-A1*Cos(2*PI*t/T)+ A2*Cos(4*PI*t/T)-A3*Cos(6*PI*t/T)+ A4*Cos(8*PI*t/T)

但し、 T：ウィンドウの時間幅

A0~A4：係数

ノイズバンド幅係数

NBFW=A0^2+0.5*(A1^2+ A2^2+ A3^2+ A4^2)

等価ノイズバンド幅

ENBW=NBFW/T

方形波

ENBW=1

ハニング

0.5 * [1-cos(2*pi*i/(N-1))]

ENBW=1.5

ハミング

0.54-0.46*cos(2*pi*i/(N-1))

ENBW=1.36

カイザーベッセル

ENBW=1.8

フラットトップ

ENBW=3.77

Triangular

1.0 - |(i-0.5*(N-1))/(0.5*(N-1))|

Welch

1-((i-0.5*(N-1))/(0.5*(N+1)))^2

ブラックマン

(0.42/0.42)-(0.5/0.42)*cos(2*pi*i/(N-1))+(0.08/0.42)*cos(4*pi*i/(N-1))

ブラックマン-ハリス

(0.35875/0.35875)-(0.48829/0.35875)*cos(pi*i/(N-1))+(0.14128/0.35875)*cos(2*pi*i/(N-1))-(0.01168/0.35875) *cos(3*pi*i/(N-1))

Parzen

1.0 - |(i-0.5*(N-1))/(0.5*(N+1))|

;--------------------------------------------------------------
wintype=3
fftoption wintype 0
window = ifft( fft( Leng( 0, 1024)+1))

temp=fft(window)
enbw=max( temp.m)

製品詳細はこちら