連続剛性測定法の原理
連続剛性測定法(CSM)のあらまし
記号の説明:
A:接触面積
h :変位
hc :接触深さ
P:法線方向の荷重
E:ヤング率
E* :複合ヤング率
H:硬度
S:試料の剛性(スチフネス)
K:複合スチフネス。
Ks :板バネ(leaf spring)のスチフネス
Kf :荷重系の枠(load frame)のスチフネス
C :コンブライアンス(C=1/S)
Cf:ロードフレームのコンブライアンス
z :振動変位
F:励起(excitation)のカ
h0 :変位振幅
F0 :励起振幅
Φ:位相角度
f:励起振動数(Hz)
ω :励起振動数(rad/sec)
ωn: 共鳴振動数
m:圧子系の質量
D:複合ダンピング
Di: 庄子系のダンピング
Ds :試料のダンピング
Dc :臨界ダンピング
1. CSMって何? 何が良いの?
試料のヤング率を決めるには接触剛性(スチフネス)を知る必要があります。
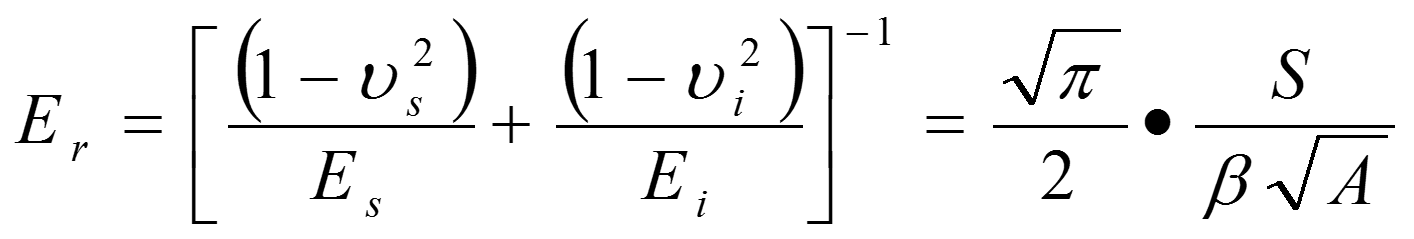
さらに硬度も接触面積を通してスチフネスSの影響を間接的に受けています。
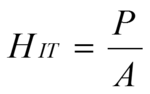
A=f(hc)
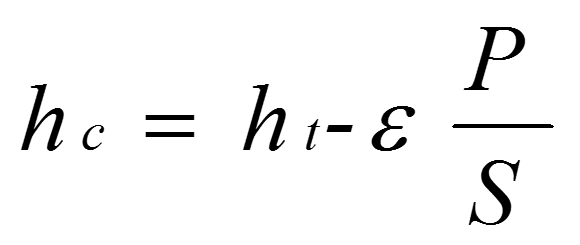
伝統的な押し込み試験(ISO14577に準拠した押し込み試験)では、このスチフネスは荷重の除荷の過程での勾配;S=dP/dhから求められます。したがって押し込み過程の最大荷重での機械特性しか求められないことになります。
CSM(continuous stiffness measurement)では、大きなスケールの直流荷重負荷(DC loading)に小さな振動を加えます。その結果として発生する変位の振動成分並びに変位と荷重の位相差を測定することで、あらゆる測定点での接触のスチフネスSとダンピングDsを計算することができます。したがってたった1回の押し込み試験から、圧子の変位の関数として連続的にヤング率と硬度を求めることができます。ガラス、セラミクス、多くの金属に対して、CSMは非常に有効です。また、その他の多くの物質についても絶対に必要な手段になります。というのも、高分子材料など多くの物質は粘弾性的であり;
- ダンピング(損失)のために(変形の)回復が時間に依存する(遅れがある)
- 荷重を減らしても圧子の変位がなお増加することもある
- 除荷曲線はパワー・ロー(ベキ乗級数)であらわせない
- (除荷曲線の)勾配は位置に敏感に依存し除荷の初期段階ではしばしば負になる
一方CSMは次のことを可能にします;
- 機械特性が荷重負荷過程で変位の連続的な関数として求められる
- (膜の厚さなど)あらかじめ知っておかなくても試験することが出来る
- 10回の押し込み試験で、充分に統計的に意味ある結果が得られる
- 粘弾性的な物質についての機械特性を求めることもできる
CSMについての本当にすばらしいことの1つは深さを検知する(depth sensing)押し込み試験のヤング率と硬度では必ず必要な圧子の面積補正関数の計算手段を劇的に簡単化しかっ精度の良いものにすることであります。基本的な手順それ自体は変わらないのですが、様々な押し込み深さでの実に多数回(~180個の押し込み試験が必要)の押し込み試験を実行する代わりに、10nm~2500nmにわたる2組と250 nmまでの1組のたかだか10回ずつの3組の押し込み試験ですみます。すなわち30個の押し込み試験で、CfとA(hc)を決めるのに必要なすべての情報を得ることが出来ます。
2. CSWの動作原理
単純調和振動子モデル:Nano lndenterシステムでは庄子執を支える板バネ(リーフスプリング、leaf spring) は横方向に非常に硬く(~104N/m)、縦方向には簡単に動きます(柔らかい) (40~80N/m)。したがって圧子の動きは1方向に限られ、この系は図1に示す単純な調和振動子系をモデルとすることができます。(各素子の)力の総和は次のような常微分方程式になります;

Kは接触系S、荷重系の枠(ロードフレーム) Cf-1とリーフスプリングKsの複合スチフネスであります;

ダンピングDも圧子系と試料の合成である複合ダッシュポットのものであります;

時間に依存する次のような力;

に対する(1)式の次の特別解を仮定します:

言い換えれば、変位は力と同じ緩動数(ω)で位相角Φだけ遅れて振動するということです。この特別解を(1)式に代入することで次の式が得られます(付録A);


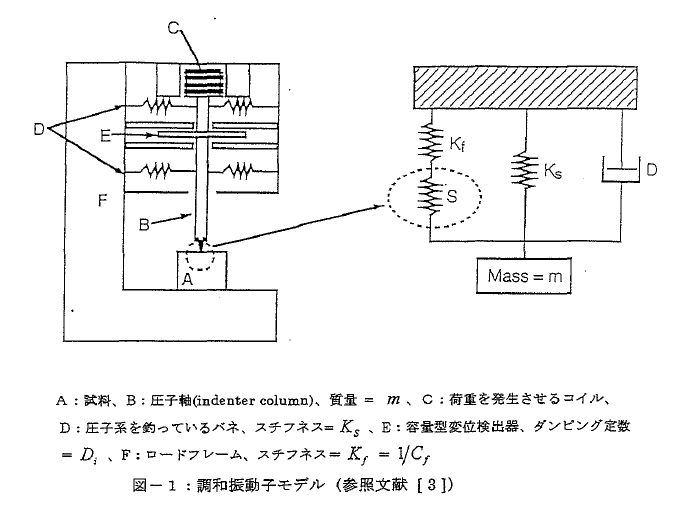
この2つの式をスチフネスとダンピングについて解けば(付録A)
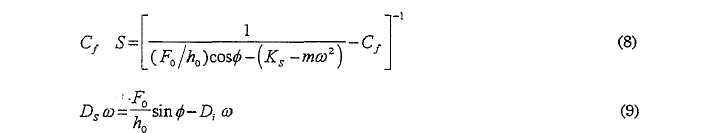
CSMの試験では、変位の振動振幅(h0)、位相角度の遅れ(Φ)と励起振動振幅(F0)を測定します。したがって、もしも機械系のパラメータCf、m、KsとDiを知れば、(8)、(9)式を使って容易にS とDsω を計算することができます。Cf は圧子の形状補正関数を求めるときに決められ、m 、KsとD,はのちに述べるダイナミック・キャリプレーションの手順で決めることができます。ここではこれらのパラメータが解っているものとします。
3. 典型的なCSW実験
典型的なCSM試験では励起振動数はf=45Hz(ω= 283rad/sec)に設定されることが多いです。励起振幅は応答である変位の振動振幅が一定(普通はlnm)になるように連続的に制御されます。変位ならびに荷重の振動振幅との位相差角度はロックイン・アンプを使って測定されます。普通の振動試験では振動系の要素(荷重など)は固定され、振動数を変えながら系の応答を測定します。
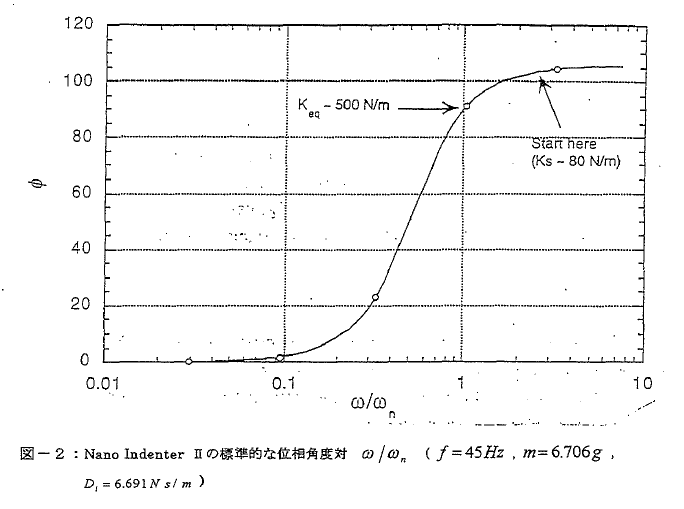
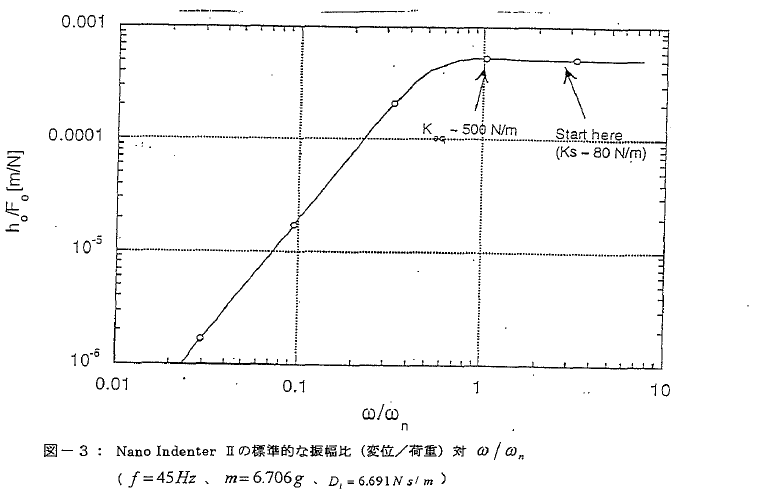
CSM試験では励起振動数は固定されていますが複合スチフネス(接触のスチフネス) Kは~ 80N/mから~5*106N/mへ増加します。この系の減衰のない自然振動数(共振振動数)は次の式で与えられます;

NanoIIシリーズの装置についてはm≒0.006kgであり、ωnは最初~91rad/secまたは18.4Hzとなります。したがって、試験の始まりでは共振振動数は励起振動数(45Hz)よりも小さくΦ>90°であります。剛性SがしたがってKが増大するにつれて、系の共振振動数は大きくなり励起振動数に近づきます。さらにωnはωを過ぎて一様に大きくなり、Φは零に近づきます。h0/F0対ω/ωnとΦ対ω/ωn の典型的な変化の様相を図-2と-3 に示します。この系の臨界(critical)ダンピングは次の式で与えられます;

ω=45Hz=283rad /secのとき、臨界ダンピングは3.4Ns/mであります。NanoIIではヘッドのダンピングは最小でも(圧子軸に国定された電極板が可動場の中心位置にあるとき)、~ 7Ns/mであります。したがって系が共振点を通過しても、系が臨界ダンピングを過ぎているので変位振幅に極値は存在しません。
図2と図3は、押し込みの過程で物理的に何が起きるかを示すものであります。実際には試験の前に電子回路で故意に荷重と変位の位相差角が零になるように設定されます。この操作が"Re-calibrate continuous stiffness option “の第4ステップであります。したがって、測定データでは位相角度は零から始まり共振点を超えて(~110° )まで増加します。測定の後で位棺角度は図2のような型に変換されなければ、すなわち共振点の上から始まり接触スチフネスが増加するにしたがって零に向かうように変えなければなりません。この変換の詳細は付録Bに述べます。
1回の押し込み試験データーファイルには次の諸変量の測定伎が含まれます;
- h, 変位
- P, 荷重
- t, 時間
- h0, 変位(振動)振幅
- Φ, 位相
- F0, 励起振幅(荷重)
CSMデータの統計についてのノート
普通は10回の試験結果について、変位軸に設定したウィンドウの幅Δhにわたって次の変数の平均値と偏差を求めます;- 変位
- Eの平均
- H の平均
- Eの標準偏差(1シグマ)
- H の標準偏差(1シグマ)
個々のウインドウ(例えば5nm)について、弾性率と硬度の平均値と標準偏差が得られます。ウインドウを越えるある範囲にわたっての統計操作をしたいとしましょう。たとえば厚さ1μmの薄膜の試験について、ウィンドウを5nmに設定して平均したとします。その結果を検証して、100~200nmにわたる広域(フィルムの厚さの10%~20%のところ)の“総体の(pooled)"平均を求めるわけです。参照文献(4)の122ベージにより、各ウインドウのサンプル個数をN、ウィンドウの数をN とします。変数xの総体の平均は、各ウィンドウの平均値に重みをかけて平均したものであります;

xの総体平均の変動(variance)は各ウインドウの変動の重み付き平均です:

xの総体の標準偏差は、総体の変動の平方根になります。
4. ダイナミック・キャリブレーション(Dynamic Calibration)
これまでは既知のものとして扱ってきた装置定数、m、Ks、Di について考えます。これらの値は庄子が何にも拘束されずに釣り下がっている自由状態を使って(S=0)、決めることができます。この状況では変位振幅の荷重振幅に対する比は;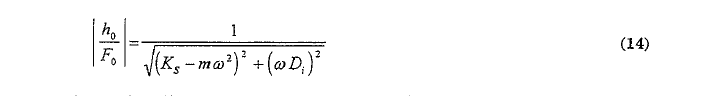
この式は(6)式で,単にK=Ksとしたものであります。
第1段階:
測定系を広い振動数範囲にわたって励起させてh0/F0を測定します。その例(h0/F0とω) を図4に示します。これらのデータに、m、Ks、Diをパラメータとして(14)式をカーブ・フィティングさせます。そのようなフィティングの例も図-4に示します。次のことが直感的に理解できるでしょう;
・ 低い振動数域では、h0/F0はスプリング定数Ksによりほとんど決まる
・ 中間の振動数域では、h0/F0はダンピングDiによりほとんど決まる
・ 高い振動数域では、h0/F0は質量mによりほとんど決まる
ほとんどの測定系でこのフィティングから、質量m とKsを決めることが出来ます。板バネのスチフネス(Ks )は電極板の間の位置に僅かに依存することもあり得ますそれは普通の変位の範囲(<3μm) では考慮するほどのことではありません。
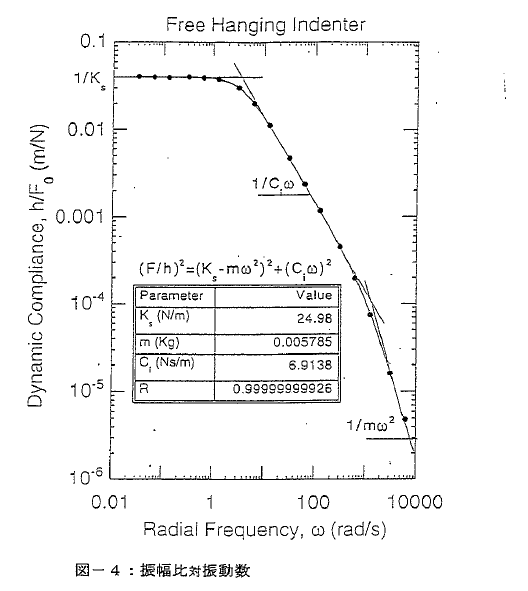
文献(3)でLucasは、Ksが60μmの範囲にわたって8N/m程度しか変わらないことを明らかにしています。もしもこの程度が問題になるような測定が課題であるのならば、文献(3)に述べられている手順でKsを間際の中の位置の関数として表すことが出来ます。単に、圧子に一定荷重を負荷してその待の変位を測ることでもKsのDC的値を知ることが出来ます。一般的にKsのDC的とAC的値はそれほど違うものではありません。
第2段階:
ダンピング(損失)定数は2枚の固定電極板の間隙の中での圧子軸固定電極の位置によって敏感に変わります。この依存を関数的に求めるには(自由状態で吊されている圧子の共振振動数に)振動数を固定してh0/F0を測定しながら、間隙の中での圧子軸電極板の位置を(荷重負荷により)変えます。(14)式をDiについて解けば;

第1段階で決められたmとKsの値を使って、間隙の中のそれぞれの位置についてDiを計算することが出来ます。これらのデータを4次の多項式で近似します;

第1項a0は、第1段階で求められたDiに殆ど等しい値であるはずです。
V. どうしてf= 45Hz、h0= 1nmを使うの? 他の値を使うときは?
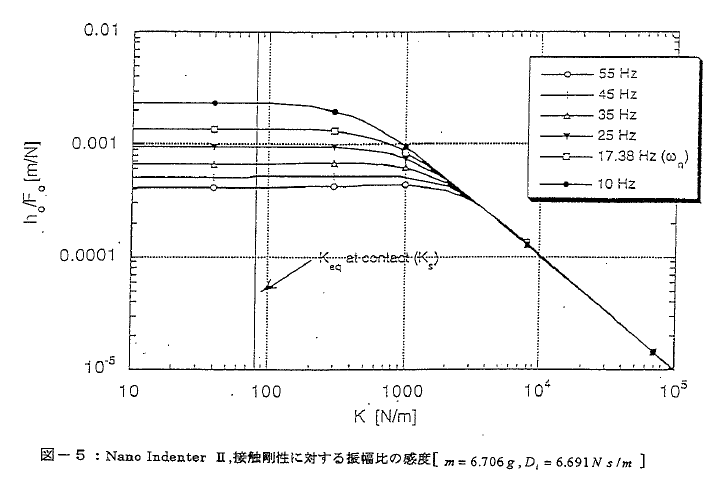
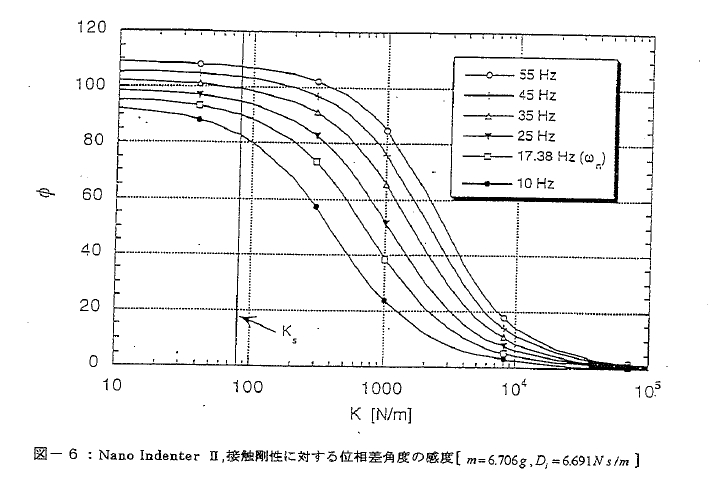
A.振動数:図-5と-6に、(これが測定の対象である)Kの変化に対するΦと
h0/F0の感度を示しました。次のことが解るでしょう;
- 試験の開始後すぐにはΦはh0/F0よりもKの変化に敏感で、これが我々が接触点の検出にΦを使う理由でもある
- Kの大きなところではΦは励起振動数によらずKの変化に敏感ではない
- Kの大きなところではh0/F0はKの変化に対し励起振動数によらず同じ感度を示す
- Φは試験開始点近傍で励起振動数が小さくなるほどKの変化により敏感になる
Kの大きなところではh0/F0とΦはいずれも励起振動数にはむしろ依存しないので、励起振動数を変える利点は表面検出の感度を高めることだけです。適当な剛さ(スチフネス)を持つ物質はどんなものでも(金属、ガラス、セラミックスなど)、圧子が表面に触れるや否や剛性が極端に増加するから、このこと(表面検出の感度)は問題になりません。
しかし柔らかな高分子物質の場合は話が別で、接触のスチフネスが~100N/mになるまでに圧子が数ミクロンも押し込まれてしまうのです。これが接触点を決めるのを難しくしています。理論的には図-6から、励起振動数を小さくすれば良いわけですが、現実にはそうもいかないことがあります。すなわちロック・イン・アンプの励起振動数を下げるとノイズレベルが上がってしまう特性とのかねあいがあります。ほとんどの物質に対して45Hzが、表面検出にからむΦの感度とロック・イン・アンプのノイズレベルのかねあいの最適値になっています。しかし表面検出の幾しい高分子試料については、励起振動数を下げるのが有効の場合も多いでしょう。
B.振幅
励起振幅は変位振幅が常にlnmになるように制御されます(フィードパック)が;
- DC荷重と干渉しないようにより小さな振幅(超低荷重)を使うのが望ましい場合が多いが、現在のロック・イン・アンプではlnmが使用に耐える最小の振幅限界
- 線形弾性の仮定から外れないように実際に可能な限り小さな振幅を常に使うべきと主張する人たちもいる
- 全体の変形が大きな場合は、振幅の増大はデータのバラツキ(雑音)を減少するからより大きな振幅を使うのが有利
Nano lndenter IIは、荷重の振幅を制御しながらの試験(F0を固定してh0を測定する)も可能です。しかし残念なことに、押し込みが深くなるにつれて変位の振幅は非常に小さくなるので変位の測定精度が悪くなります。これ(F0を固定)が有効なのは、剛性が深さによって大きく変わらない柔らかな高分子物質の時だけです。フィードパック・ループを使わなければ、データのバラツキを押さえることが出来るからです。
付録A:(6~9)式の導出
(6)と(7)式は振動解析には基本的なものであり、この型の式は振動論あるいは微分方程式のどんな初級コースの教本にも見られます。例えば、参照文献(2)です。
2階の常微分方程式;

の特別解の1つに次の型があります;

すなわち変位は励起と同じ振動数で振動し位相がΦだけ遅れます。(5)式の1次と2次の微分を求めます;

これを(1)に入れて;
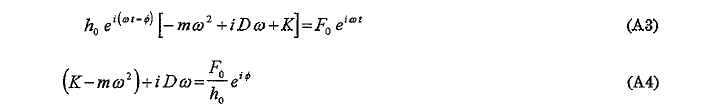
オイラーの関係式;
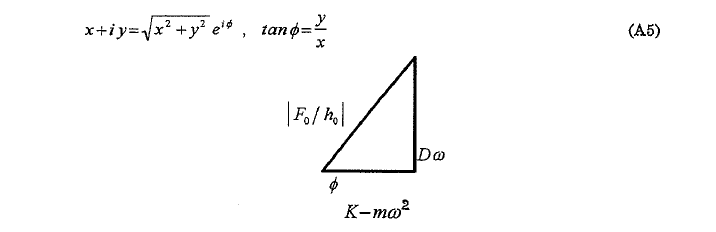
を使って、(A4)は次ぎのようになります:
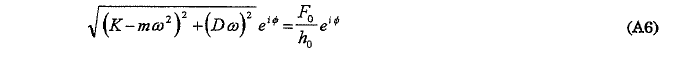
これより:


スチフネスとダンピングは、(6)と(7)式を連立で解いて求められます。最初にK について(6)式を解いて;

オイラーの関係式を使えばDω は;

したがって(A7)式は;

Kには接触の剛性S、荷重系フレームのコンブライアンスCf-1と板バメのバネ定数が含まれることを思い出して下さい;

このK を(A9)式に入れてSについて解きます:
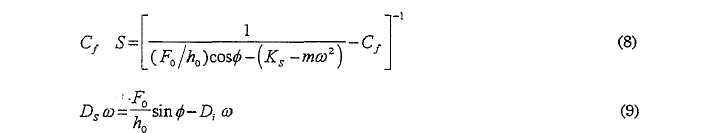
複合ダンピングを展開して(A8)式から、直接、ダンピング(損失)項が求められます;
付録B : 位相差測定値の修正
この修正はサブルーチンプログラム“Calcld"で実行されます。その目的は、0°から110°に向かう位相角度の測定値(Φexp ) を図3に示したような物理的に意味のあるΦに変換することです。
1. Φ’exp=-Φexpとして、0°から-110°に向かうΦ’exp を求める
2. 圧子系の動力学から接近過程での位相角度を計算する;
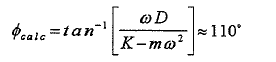
3. 接近過程の位相角度の測定伎の平均、Oapp を求める(零に近いはず)
4. これら接近過程の位相角度の計算値と実測値の差を求める;
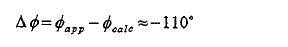
5. 次の式を使いすべての位相角度のデータA を修正する;
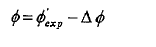
Φ’exp は0°から-110°に向って変化するので、Φは110°から0°に向かうことになります。
参照文献
1. Oliver and Pharr," An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments." Journal of Materials Research,Vol. 7,No.6,p1564.1583,June,1992.
2. Thomson,Theory of Vibrations Applications, p.51,1988.
3. Lucas,An Experimental Investigation of Creep and Viscoelastic Properties using Depth-Sensing Indentation Techniques,Ph.D dissertation,University of Tennessee,Knoxville,May,1997.
4. Figliola and Beasley,Theory and Design for Mechanical Measurements,p. 122,1991.