ナノインデンターを用いた微小領域における粘弾性試験
概要
ナノインデンターを用いて微小領域における、高分子の粘弾性の試験を行うことが可能です。CSMを利用し、加振周波数を変更した場合の貯蔵モジュラス(E’),損失モジュラス(E”),損失正接(LF)を評価します。それぞれのパラメータは下記の数式で計算されます。

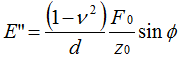
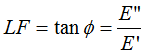 ・・・(1)
・・・(1)
F0:振動荷重,z0:振動振幅,Φi:位相シフト,d:接触面積,ν:ポアソン比
なお、本測定においては50nm程度の大きな振幅を印加します。そのため、接触面積を一定に保つためにフラットパンチ圧子を使用します。

図1)直径50umのフラットパンチ圧子
原理
動的押し込み試験の原理は、弾性接触モデルおよびDMA試験において高分子の機械的な挙動を理解するために用いられるような構成の両方によって得られます。Ian Sneddonは、平坦な表面を用いて軸対称の圧子に対する荷重, 変位, 弾性定数の間の一般的な関係を初めて導きました[2]。Oliver, Pharr, およびBrotzenは、Sneddonの関係が圧子の幾何学形状と事実上無関係であることを示しました[3]。これらの関係は通常、計装化押し込み試験のデータを解析するために用いられます。
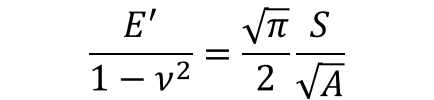 ・・・(2)
・・・(2)
ここで、E’ は材料の貯蔵弾性率、νはポアソン比、Sは接触剛性、Aは接触面積をそれぞれ表します。材料の応答が十分に弾性的である場合、貯蔵弾性率はよく知られているヤング率と一致します。後に、Loubet, Lucas, およびOliverはDMAと同じ構成要素の材料を用いて、損失弾性率(E'')と接触減衰(Dsω)との間に相似関係があることを推論しています[4]。
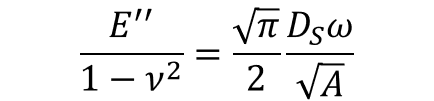 ・・・(3)
・・・(3)接触面積が例え未知であっても損失正接では除算されるため、動的押し込み試験において損失正接が非常に有効です。
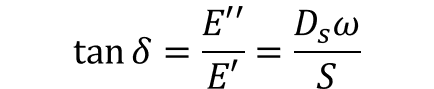 ・・・(4)
・・・(4)
このようにして、動的押し込み試験を用いた高分子の複素弾性率は接触剛性Sと減衰Dsωを計測すれば求められます。
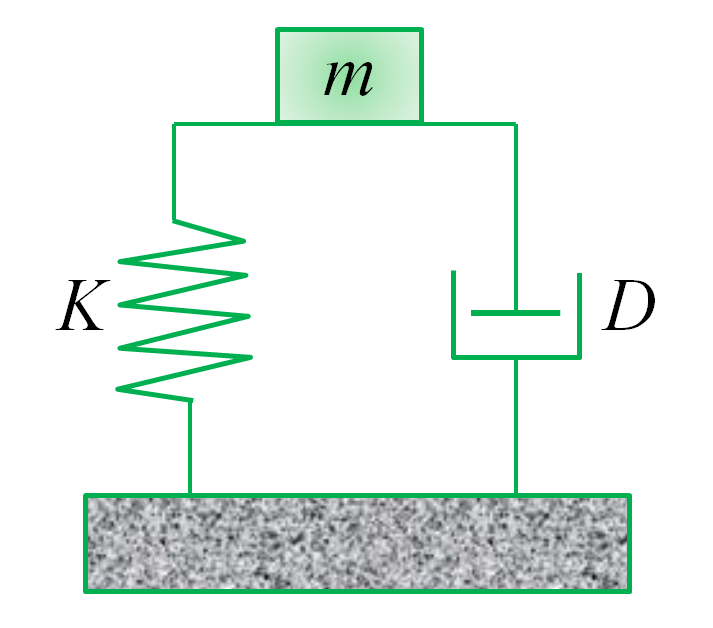
図2)インデンテーションシステム単体またはサンプルとの接触をモデル化するための調和振動子
iNanoナノインデンターシステムは図2で示すような調和振動子モデルのように振る舞うように慎重に設計されてきました。そのため、荷重の振幅(F0), 角周波数(ω)を装置が発生させ、変位の振幅(z0), 位相シフト(Φ)を計測すれば下式で表されるすべての値が求められることになります。
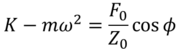 ・・・(5)
・・・(5)
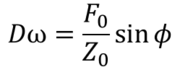 ・・・(6)
・・・(6)
圧子がフリーの状態(どの材料にも接していない状態)の時、K, D, mはナノインデンター自身の剛性, 減衰, 質量になります。それぞれKi, Di, miと表現します。実際に工場で校正を行う際には、圧子がフリーの状態で振動させることによりKi, Di, miを求めます。実際に圧子が測定対象に接触するとK, D, mのパラメータはナノインデンター自身と接触によりものの両方の影響を含みます。このようにしてF0, z0, Φは接触の影響を切り分けるために装置の影響を既知のものとして補正することが必要です。実験の際には、接触剛性は式2を用いて下記の通り装置の値を除くようにして求められます。
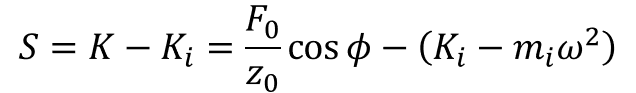 ・・・(7)
・・・(7)
式3において、接触の減衰から装置自体の減衰を差し引き、サンプルの減衰を求められます。
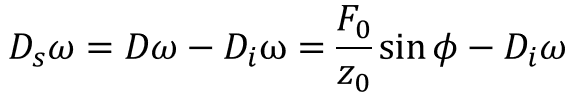 ・・・(8)
・・・(8)
高分子材料の測定を行う上で、フラットパンチ圧子を用いる利点は2つあげられます。1つ目は線形粘弾性の仮定と一致するような変形を起こさせる点にあります。2つめは、式2,3で登場する接触面積(A)が明確で、かつ押し込み深さに依存しないことです。一般的に、圧子先端の直径はサンプルの微細構造、必要な空間分解能、材料特性および装置の感度によって選択すべきです。必要な空間分解能は材料の微細構造によって多くの場合は決められてしまいます。つまり、その材料が機械的な振る舞いを決定する時に関連する構造をカバーするのに、圧子の面積は十分な大きさであることが必要です。しかし、圧子の面積が大きすぎることによって、圧子とサンプルとが完全に接触し振動試験を行えるような荷重を装置が発生されられないという事態は避けなければないりません。より高い空間分解能を得るためには、先端のより小さい圧子を選択すべきです。その上で、装置の応答ではなく測定の応答がきちんと計測できるほど十分な接触を得るために、圧子先端の直径は適切な大きさである必要があります。
従来手法との比較
高可塑化ポリ塩化ビニル (HP-PVC)を測定しました。この材料は振動ノイズ対策用マットによく用いられています。サイズは約15cm角、厚み6mmの市販品を装置にセットできる2cm角程度に切断し、樹脂包埋した後に機械研磨しました(図3)。

図3)樹脂包埋されたHP-PVC
装置はiNanoナノインデンターを用いて周波数に対する複素弾性率を計測しました。これらの測定に対し、先端直径52.5μm、開き角度60°のフラットパンチ圧子を装置にとりつけています。iNanoを用いた動的粘弾性測定は下記のように行われます。なお、全ての試験は室温で行っています。
- 圧子の面はサンプルの表面に完全接触させます。
- 100Hzで50nmの振幅(z0)になるように動的荷重の振幅(F0)を決定します。
この荷重は他の周波数でも同じ値を用います。 - 周波数を掃引し、各周波数における変位振幅(z0)および位相シフト(Φ)を求めます。
- 各周波数で式7および式8から計算される接触剛性と減衰を求めます。
そこから式2,3,4を用いて貯蔵弾性率、損失弾性率、損失正接を求めました。
上記のサイクルを測定場所を変えて計15点行いました。
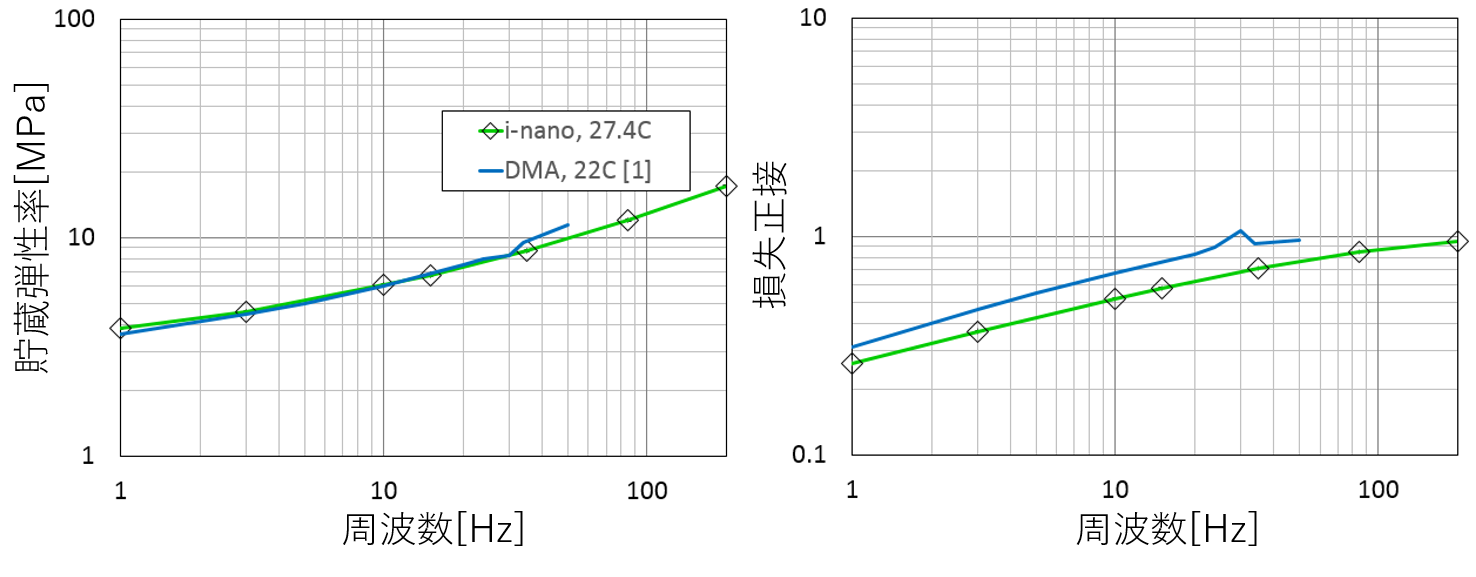
図4)貯蔵弾性率(左)と損失正接(右)
緑のラインがナノインデンターによる測定、青のラインがDMA(マクロな手法)による測定
図4は、ナノインデンターを用いた試験(緑の曲線)[1]とDMA(青の曲線)を比較したグラフです。ナノインデンターによる試験は非常に高い再現性があり、エラーバー(標準偏差)がかすかに見える程度です。計算式の微妙な違いやサンプルの見ている領域の違いから測定手法間で違いが現れています。DMAの30Hzの結果に"ぐらつき"が見受けられますが、装置由来の計算が不十分であったことによるものと言われています。
HP-PVCは周波数依存性が強く現れるサンプルです。期待通り、損失正接(tanδ)は特に高くなっています。高い周波数では損失正接が1に近づいています。これはこの材料が多くのエネルギーを減衰させ、材料自身がエネルギーを蓄えて弾性的になることを示しています。周波数または温度に対して損失正接(tanδ)がピークを持つ場合、材料におけるガラス転移等の相転移することを意味します。ドメインが十分大きい場合には、異なる相転移に一致したマルチピークが損失正接に見られます。HP-PVCについては、周波数の上昇に応じて損失正接が右肩上がりになっています。これは材料が相転移に近づいていっていることを意味します。
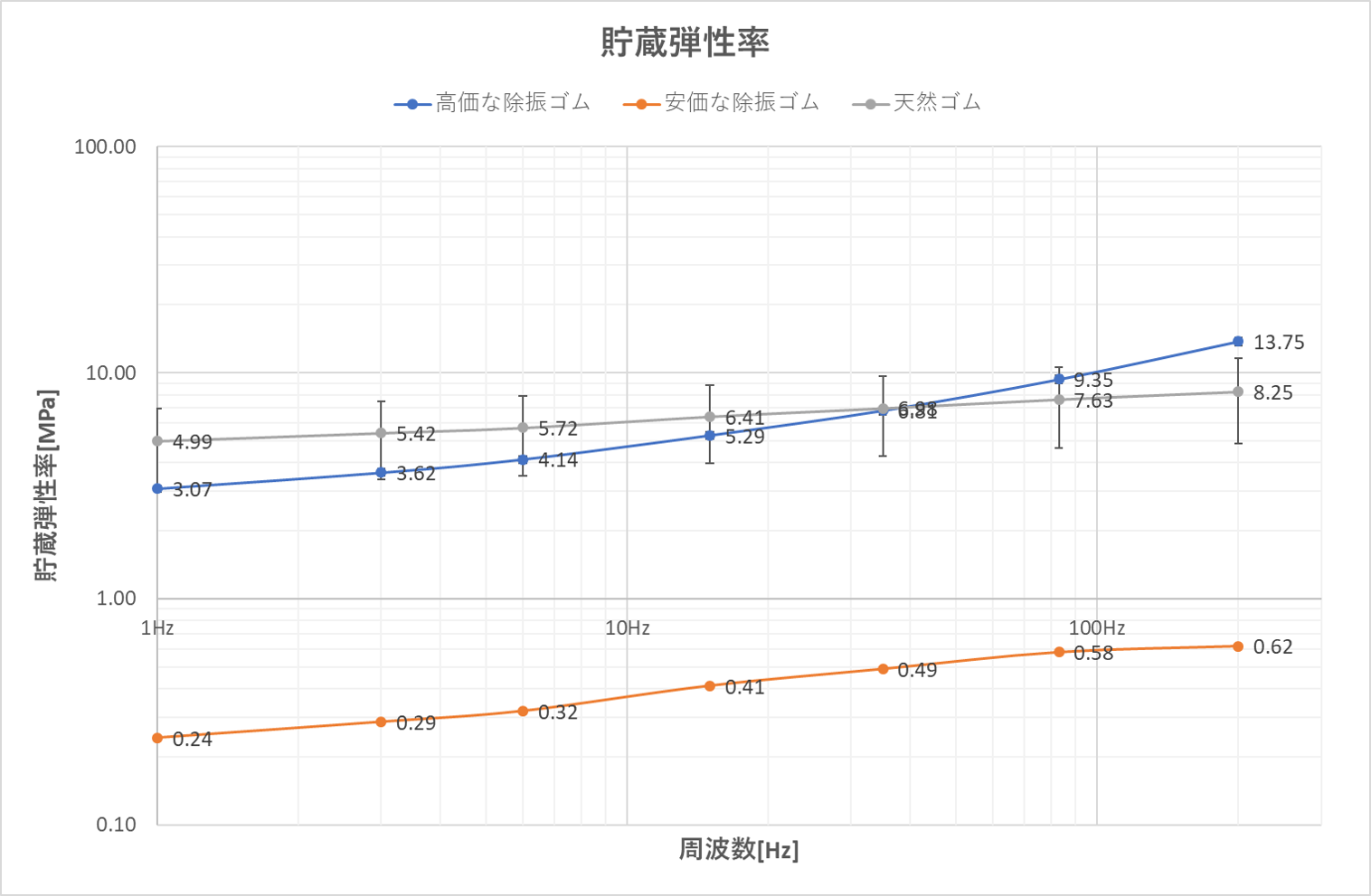
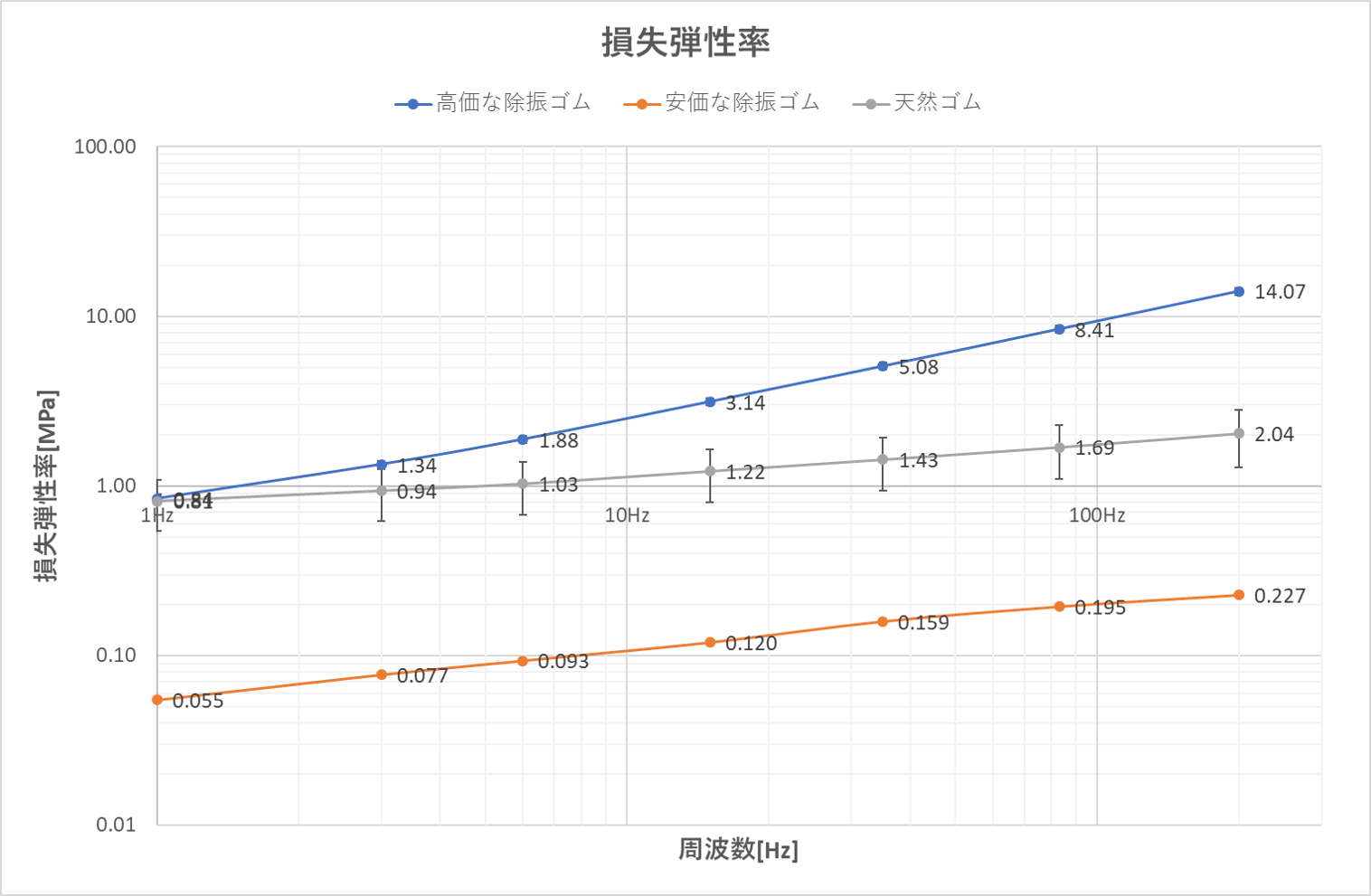
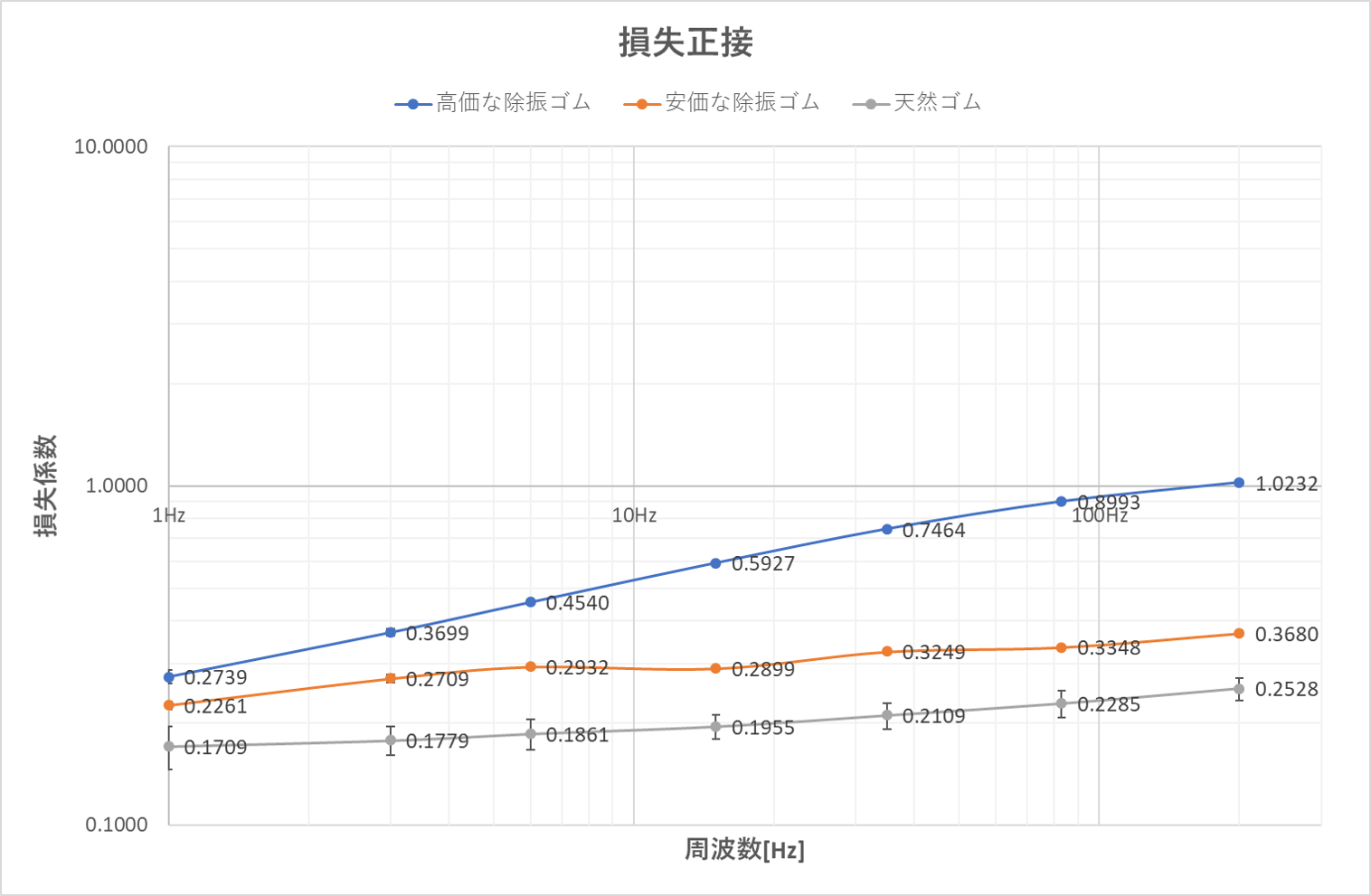
測定例1
下記の例は2種類の除振用のゴム2種類および天然ゴムの特性を比較したものです。特性が明確に現れています。高価なゴムが周波数の上昇とともに損失弾性率・損失係数が大きくなっており、振動が加わった際に振動を逃がす効果が高いことが判ります。安価なゴムは天然ゴムに比べれば除振性能を有していることがわかります。
---関連製品
- <参考>
- Herbert, E.G., Oliver, W.C., and Pharr, G.M., ‘‘Nanoindentation and the Dynamic Characterization of Viscoelastic Solids,’’ Journal of Physics D: Applied Physics 41:1–9 (2008).
- Sneddon, I.N., ‘‘The Relation Between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile,’’ International Journal of Engineering Science 3:47–56 (1965).
- Pharr, G.M., Oliver, W.C., and Brotzen, F.R., “On the Generality of the Relationship Among Contact Stiffness, Contact Area, and Elastic Modulus During Indentation, Journal of Materials Research 7(3):613–617 (1992).
- Loubet, J.-L., Lucas, B.N., and Oliver, W.C., ‘‘Some Measurements of Viscoelastic Properties with the Help of Nanoindentation,’’ NIST Special Publication 896 31(1995).